题目内容
20．已知对任意的a∈[-1，1]，函数f（x）=x2+（a-4）x+4-2a的值总大于0，则x的取值范围是（ ）| A． | x＜1或x＞3 | B． | 1＜x＜3 | C． | 1＜x＜2 | D． | x＜2或x＞3 |
分析 把二次函数的恒成立问题转化为y=a（x-2）+x2-4x+4＞0在a∈[-1，1]上恒成立，再利用一次函数函数值恒大于0所满足的条件即可求出x的取值范围．
解答 解：原题可转化为关于a的一次函数y=a（x-2）+x2-4x+4＞0在a∈[-1，1]上恒成立，
只需$\left\{\begin{array}{l}{（-1）（x-2）+{x}^{2}-4x+4＞0}\\{x-2+{x}^{2}-4x+4＞0}\end{array}\right.$⇒$\left\{\begin{array}{l}{x＞3或x＜2}\\{x＞2或x＜1}\end{array}\right.$⇒x＜1或x＞3．
故选：A．
点评 本题的做题方法的好处在于避免了讨论二次函数的对称轴和变量间的大小关系，而一次函数在闭区间上的最值一定在端点处取得，所以就把解题过程简单化了．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
11．设O是△ABC的内心，AB=c，AC=b，若$\overrightarrow{AO}={λ_1}\overrightarrow{AB}+{λ_2}\overrightarrow{AC}$，则（ ）
| A． | $\frac{λ_1}{λ_2}=\frac{b}{c}$ | B． | $\frac{λ_1^2}{λ_2^2}=\frac{b}{c}$ | C． | $\frac{λ_1}{λ_2}=\frac{c^2}{b^2}$ | D． | $\frac{λ_1^2}{λ_2^2}=\frac{c}{b}$ |
8．设点P（x，y）在椭圆4x2+y2=4上，则x+y的最大值为（ ）
| A． | 3 | B． | -3 | C． | 4 | D． | $\sqrt{5}$ |
9．某次数学测验后，数学老师统计了本班学生对选做题的选做情况，得到如表数据：（单位：人）
（I）请完成题中的2×2列联表；并根据表中的数据判断，是否有超过97.5%的把握认为选做“坐标系与参数方程”或“不等式选讲”与性别有关？
（II）经过多次测试后，甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间[5，7]内一个随机值（单位：分钟），解答一道“不等式选讲”所用的时间为区间[6，8]内一个随机值（单位：分钟），试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率．
附表及公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
| 坐标系与参数方程 | 不等式选讲 | 合计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 合计 | 30 | 20 | 50 |
（II）经过多次测试后，甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间[5，7]内一个随机值（单位：分钟），解答一道“不等式选讲”所用的时间为区间[6，8]内一个随机值（单位：分钟），试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率．
附表及公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
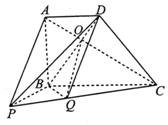如图，在四棱锥P-ABCD中，ABCD是梯形，AD∥BC，∠ABC=90°，平面PAB⊥平面ABCD，PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC．