题目内容
1.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且$\overrightarrow{a}$•$\overrightarrow{b}$=-3,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$.分析 由条件利用两个向量的数量积的定义求得cosθ的值,可得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ 的值.
解答 解:∵向量$\overrightarrow{a}$与$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且$\overrightarrow{a}$•$\overrightarrow{b}$=-3,设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,
则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-3}{2×3}$=-$\frac{1}{2}$,∴θ=$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$.
点评 本题主要考查两个向量的数量积的定义,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.设O是△ABC的内心,AB=c,AC=b,若$\overrightarrow{AO}={λ_1}\overrightarrow{AB}+{λ_2}\overrightarrow{AC}$,则( )
| A. | $\frac{λ_1}{λ_2}=\frac{b}{c}$ | B. | $\frac{λ_1^2}{λ_2^2}=\frac{b}{c}$ | C. | $\frac{λ_1}{λ_2}=\frac{c^2}{b^2}$ | D. | $\frac{λ_1^2}{λ_2^2}=\frac{c}{b}$ |
9.某次数学测验后,数学老师统计了本班学生对选做题的选做情况,得到如表数据:(单位:人)
(I)请完成题中的2×2列联表;并根据表中的数据判断,是否有超过97.5%的把握认为选做“坐标系与参数方程”或“不等式选讲”与性别有关?
(II)经过多次测试后,甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间[5,7]内一个随机值(单位:分钟),解答一道“不等式选讲”所用的时间为区间[6,8]内一个随机值(单位:分钟),试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率.
附表及公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 坐标系与参数方程 | 不等式选讲 | 合计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 合计 | 30 | 20 | 50 |
(II)经过多次测试后,甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间[5,7]内一个随机值(单位:分钟),解答一道“不等式选讲”所用的时间为区间[6,8]内一个随机值(单位:分钟),试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率.
附表及公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
16.“x+y=3”是“x=1且y=2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也必要条件 |
11.在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为45°,若E是PB的中点,则异面直线DE与PA所成角的余弦值为( )
| A. | $\frac{{3\sqrt{10}}}{20}$ | B. | $\frac{{\sqrt{10}}}{20}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
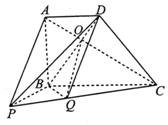 如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.
如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.