题目内容
3．双曲线Γ中心在坐标原点，焦点在坐标轴上，又Γ的实轴长为4，且一条渐近线为y=2x，求双曲线Γ的标准方程．分析 渐近线方程y=-2x，实轴长为4，进而可知b的关系，判断焦点坐标所在的轴，即可求解双曲线的方程．
解答 解：双曲线Γ中心在坐标原点，焦点在坐标轴上，又Γ的实轴长为4，且一条渐近线为y=2x，
可得双曲线的焦点坐标在x轴时，a=4，b=8，双曲线方程为：$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{64}=1$；
双曲线的焦点坐标在y轴时，a=4，b=2，双曲线方程为：$\frac{{y}^{2}}{16}-\frac{{x}^{2}}{4}=1$；
点评 本题主要考查了双曲线的简单性质．考查了学生对双曲线方程基础知识的掌握和运用．
练习册系列答案
全优点练单元计划系列答案
相关题目
13．已知集合M={x|x-2＞0，x∈R}，N={y|y=$\sqrt{{x}^{2}+1}$，x∈R}，则M∩N=（ ）
| A． | {x|x≥1} | B． | {x|1≤x＜2} | C． | {x|x＞2} | D． | {x|x＞2或x＜0} |
14．$\frac{1}{3}$[$\frac{1}{2}$（2a+8b）-（4a-2b）]等于（ ）
| A． | 2a-b | B． | 2b-a | C． | b-a | D． | -（ b-a ） |
8．在△ABC中，角A，B，C所对边分别为a，b，c，且c=4$\sqrt{2}$，B=$\frac{π}{4}$，面积S=2，则b等于（ ）
| A． | $\frac{\sqrt{113}}{2}$ | B． | 5 | C． | $\sqrt{41}$ | D． | 25 |
12．
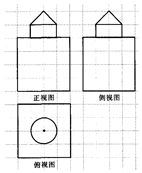如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）| A． | $（{2\sqrt{2}+2}）π+96$ | B． | $（{2\sqrt{2}+1}）π+96$ | C． | $（{\sqrt{2}+2}）π+96$ | D． | $（{\sqrt{2}+1}）π+96$ |