题目内容
设函数f(x)＝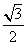
－
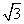sin2ωx－sin ωxcos ωx(ω＞0)，且y＝f(x)的图象的一个对称中心到最近的对称轴的距离为
，
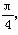(1)求ω的值；
(2)求f(x)在区间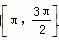
上的最大值和最小值．
解析：(1)f(x)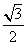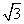＝－sin2ωx－sin ωxcos ωx
＝－×
－
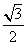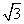sin 2ωx
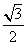＝cos 2ωx－sin 2ωx＝－sin
.
依题意知
，ω>0，所以ω＝1.
(2)由(1)知f(x)＝－sin
.
.
所以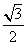－≤sin
≤1.所以－1≤f(x)≤.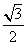
故f(x)在区间
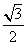上的最大值和最小值分别为，－1.
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
．∃x∈R，cos x≥1 B．∀x∈R，cos x＜1
，则此时该船到灯塔S的距离为______海里(结果保留最简根式)．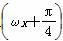
(其中x∈R，A＞0，ω＞0)的最大值为
2，最小正周期为8.
,4，O为坐标原点，求cos∠POQ的值．
(x∈R)的图象向左平移m(m>0)个单位长度后，所得到的图象关于y轴对称，则m的最小值是( )
(A＞0
，ω＞0，x∈R)的最小正周期为2，且f(0)＝
，则函数f(3)＝( )
B.
C.
D.
，则圆O的半径R＝________.