题目内容
10.在空间直角坐标系O-xyz中,点(3,-1,m)平面Oxy对称点为(3,n,-2),则m+n=1.分析 在空间直角坐标系O-xyz中,点(x,y,z)平面Oxy对称点为(x,y,-z).
解答 解:∵在空间直角坐标系O-xyz中,
点(3,-1,m)平面Oxy对称点为(3,n,-2),
∴m=2,n=-1,
∴m+n=2-1=1.
故答案为:1.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意空间直角坐标系的性质的合理运用.

练习册系列答案
相关题目
15.抛物线y=4-x2与直线y=4x的两个交点为A、B,点P在抛物线上从A向B运动,当△PAB的面积为最大时,点P的坐标为( )
| A. | (-3,-5) | B. | (-2,0) | C. | (-1,3) | D. | (0,4) |
19.定义在(0,$\frac{π}{2}$),上的函数f(x),f′(x)是导函数,满足f(x)<f′(x)tanx,则下列表达式正确的是( )
| A. | $\sqrt{3}$•f($\frac{π}{4}$)>$\sqrt{2}$•f($\frac{π}{3}$) | B. | f(1)>2•f($\frac{π}{6}$)•sin1 | C. | $\sqrt{2}$•f($\frac{π}{6}$)>f($\frac{π}{4}$) | D. | $\sqrt{3}$•f($\frac{π}{6}$)>f($\frac{π}{3}$) |
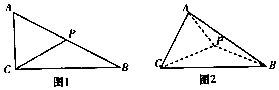 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.