题目内容
在极坐标系中,曲线ρ=2coosθ与ρ=1交于A,B两点,则|AB|= .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:曲线ρ=2coosθ化为ρ2=2ρcosθ,可得x2+y2=2x,ρ=1化为x2+y2=1,联立解得即可得出.
解答:
解:曲线ρ=2coosθ化为ρ2=2ρcosθ,∴x2+y2=2x,
ρ=1化为x2+y2=1,
联立解得
,
∴|AB|=
.
故答案为:
.
ρ=1化为x2+y2=1,
联立解得
|
∴|AB|=
| 3 |
故答案为:
| 3 |
点评:本题考查了极坐标化为直角坐标方程、圆的公共弦长,属于基础题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
已知函数f(x)=|(x-1)
|,若存在x1,x2∈[a,b],且x1<x2,使f(x1)≥f(x2)成立 则以下对实数a、b的描述正确的是( )
| 1 |
| 3 |
| A、a<1 | B、a≥1 |
| C、b≤1 | D、b≥1 |
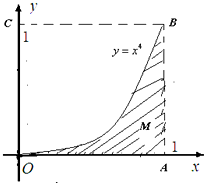 Monte-Carlo方法在解决数学问题中有广泛的应用.下面是利用Monte-Carlo方法来计算定积分.考虑定积分
Monte-Carlo方法在解决数学问题中有广泛的应用.下面是利用Monte-Carlo方法来计算定积分.考虑定积分