题目内容
函数y=tan(x-
)的单调递增区间是 .
| π |
| 4 |
考点:正切函数的图象
专题:三角函数的图像与性质
分析:根据正切函数的图象与性质,即可求出函数y=tan(x-
)的单调递增区间.
| π |
| 4 |
解答:
解:根据正切函数的图象与性质,
令-
+kπ<x-
<
+kπ,k∈Z;
得:-
+kπ<x<
+kπ,k∈Z,
∴函数y=tan(x-
)的单调递增区间是
(-
+kπ,
+kπ),k∈Z.
故答案为:(-
+kπ,
+kπ),k∈Z.
令-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
得:-
| π |
| 4 |
| 3π |
| 4 |
∴函数y=tan(x-
| π |
| 4 |
(-
| π |
| 4 |
| 3π |
| 4 |
故答案为:(-
| π |
| 4 |
| 3π |
| 4 |
点评:本题考查了正切函数的图象与性质的应用问题,解题时应利用正切函数的图象与性质,列出不等式,求出解集来.

练习册系列答案
相关题目
空间两条异面直线是指它们( )
| A、没有公共点 |
| B、不在同一平面内 |
| C、分别在两个不同的平面内 |
| D、不同在任何一个平面内 |
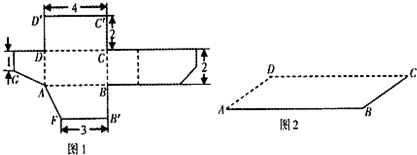 某长方体截去一个三棱锥后,形成的几何体的平面展开图的一部分如图1所示.
某长方体截去一个三棱锥后,形成的几何体的平面展开图的一部分如图1所示.