Question

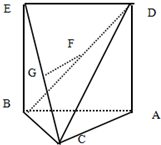如图5，三角形 A BC中，AC=BC=

2

2

，A B ED是边长为1的正方形，B E⊥底面 A BC，若G、F分别是 EC、BD的中点．
（1）求证：GF∥平面 A BC；
（2）求三棱锥 B-AEC的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：空间位置关系与距离

分析：（1）取BC的中点M，AB的中点N，连结GM、FN、MN，通过证明MNFG为平行四边形，利用直线与平面平行的判定定理证明GF∥平面ABC．
方法2：连接EA，证明GF∥AC，利用直线与平面平行的判定定理证明GF∥平面ABC．
（2）利用BE⊥底面ABC，求出高BE，利用V_B-AEC=V_E-ABC 求出几何体的体积．

解答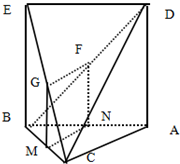： 解（1）：取BC的中点M，AB的中点N，连结GM、FN、MN   …（1分）
∵G、F分别是EC和BD的中点
∴GM∥BE，且GM=

1

2

BE，
NF∥DA，且NF=

1

2

DA…（3分）
又∵ADEB为正方形∴BE∥AD，BE=AD
∴GM∥NF且GM=NF   …（4分）
∴MNFG为平行四边形…（5分）
∴GF∥MN，…（6分）
又 MN?平面ABC，GF?平面ABC
∴GF∥平面ABC…（7分）
方法2：连接EA               …（1分）
∵ADEB为正方形，F是BD的中点，
∴EA交BD于点F       …（3分）
∴AF=FE（或者F为AE的中点） …（4分）
∵EG=GC（或者G为CE的中点），
∴GF∥AC，…（5分）
又 AC?平面ABC，GF?平面ABC，
∴GF∥平面ABC   …（7分）
（2）BE⊥底面ABC
∴BE是三棱锥E-ABC的高且BE=1   …（9分）
∴V_B-AEC=V_E-ABC …（12分）
=

1

3

S△ABC•BE=

1

3

(

1

2

×

2

2

×

2

2

)×1=

1

12

…（14分）

点评：本题考查直线与平面平行的判定定理的应用，棱锥的条件的求法，考查空间想象能力以及逻辑推理能力、计算能力．