题目内容
已知回归直线通过样本点的中心,若x与y之间的一组数据:则y与x的线性回归方程为
=
x+
必过点(注:
=
,
=
-
)( )
| ∧ |
| y |
| ∧ |
| b |
| ∧ |
| a |
| ∧ |
| b |
| |||||||
|
| ∧ |
| a |
. |
| y |
| ∧ |
| b |
. |
| x |
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
A、(
| ||
| B、(1,2) | ||
| C、(2,2) | ||
D、(
|
考点:线性回归方程
专题:计算题,概率与统计
分析:求出x、y的平均值,回归直线方程一定过样本的中心点(
,
),代入可得答案.
. |
| x |
. |
| y |
解答:
解:回归直线方程一定过样本的中心点(
,
),
=
=
,
=
=4,
∴样本中心点是(
,4),
则y与x的线性回归方程y=bx+a必过点(
,4),
故选:A.
. |
| x |
. |
| y |
. |
| x |
| 0+1+2+3 |
| 4 |
| 3 |
| 2 |
. |
| y |
| 1+3+5+7 |
| 4 |
∴样本中心点是(
| 3 |
| 2 |
则y与x的线性回归方程y=bx+a必过点(
| 3 |
| 2 |
故选:A.
点评:本题考查平均值的计算方法,回归直线的性质:回归直线方程一定过样本的中心点(
,
).
. |
| x |
. |
| y |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=lnx-
的零点所在的大致区间是( )
| 2 |
| x |
| A、(1,2) | ||
| B、(2,3) | ||
C、(1,
| ||
| D、(e,+∞) |

 如图5,三角形 A BC中,AC=BC=
如图5,三角形 A BC中,AC=BC=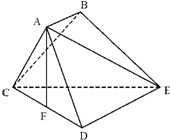 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点. 如图,F1,F2是双曲线C:
如图,F1,F2是双曲线C: