题目内容
已知等差数列{an}满足a2=2，a4=8
（1）求数列{an}的通项公式
（2）若数列{an}的前n项和为Sn，求S8．
（1）求数列{an}的通项公式
（2）若数列{an}的前n项和为Sn，求S8．
考点：等差数列的前n项和,等差数列的通项公式
专题：等差数列与等比数列
分析：（1）由已知数据易得数列{an}的公差d，进而可得a1，可得通项公式；
（2）吧a1=-1，d=3代入等差数列的求和公式可得．
（2）吧a1=-1，d=3代入等差数列的求和公式可得．
解答：
解：（1）设数列{an}的公差为d，
则由题意可得a4-a2=2d=6，
代入数据可解得d=3，
∴a1=a2-d=2-3=-1，
∴数列{an}的通项公式为an=-1+（n-1）×3=3n-4；
（2）由（1）知a1=-1，d=3，
∴S8=8a1+
d=76
则由题意可得a4-a2=2d=6，
代入数据可解得d=3，
∴a1=a2-d=2-3=-1，
∴数列{an}的通项公式为an=-1+（n-1）×3=3n-4；
（2）由（1）知a1=-1，d=3，
∴S8=8a1+
| 8×7 |
| 2 |
点评：本题考查等差数列的通项公式和求和公式，属基础题．
练习册系列答案
全优点练单元计划系列答案
相关题目
已知
=（1，5，-2），
=（3，1，z），若
⊥
，
=（x-1，y，-3），且
⊥面ABC，则
=（ ）
| AB |
| BC |
| AB |
| BC |
| PB |
| BP |
| PB |
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
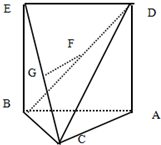如图5，三角形 A BC中，AC=BC=
如图，F1，F2是双曲线C：