Question

16．已知点O在△ABC内部一点，且满足2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$，则三角形△AOB，△BOC，△AOC的面积之比依次为（　　）

• A． 4：2：3
• B． 2：3：4
• C． 4：3：2
• D． 3：4：5

Answer 1

分析 延长OA，OB，OC，使OD=2OA，OE=3OB，OF=4OC，结合已知可得O是△DEF的重心，故△DOE，△EOF，△DOF的面积相等，进而得到答案．

解答 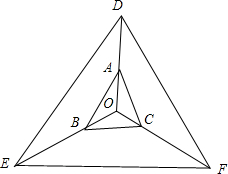解：延长OA，OB，OC，使OD=2OA，OE=3OB，OF=4OC，
如图所示：
∵2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$，
∴$\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}=\overrightarrow{0}$，
即O是△DEF的重心，
故△DOE，△EOF，△DOF的面积相等，
不妨令它们的面积均为1，
则△AOB的面积为$\frac{1}{6}$，△BOC的面积为$\frac{1}{12}$，△AOC的面积为$\frac{1}{8}$，
故三角形△AOB，△BOC，△AOC的面积之比依次为：$\frac{1}{6}$：$\frac{1}{12}$：$\frac{1}{8}$=4：2：3，
故选：A

点评 本题考查的知识点是三角形面积公式，三角形重心的性质，平面向量在几何中的应用，难度中档．