题目内容
4.设m,n是两条不同的直线,α,β是两个不同的平面( )| A. | 若m丄n,n∥α,则m丄α | B. | 若m∥n,n丄β,则m丄β | ||
| C. | 若m∥β,β 丄a,则m丄a | D. | 若 m 丄 n,n丄β,β丄a,则 m丄 a |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:对于A,若m丄n,n∥α,则m与α相交、平行或m?α,故不正确;
对于B,若m∥n,n丄β,则m⊥β,故正确;
对于C,若m∥β,β 丄α,则m丄α不一定成立,故不正确;
对于D,若m丄n,n丄β,β丄α,则m与α相交、平行或m?α,故不正确.
故选:B.
点评 本题考查空间直线与平面,平面与平面的位置关系的判定.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
16.不等式log2|2+x|≤1的解集为( )
| A. | {x|x≥0} | B. | {x|x≥-2} | C. | {x|0≤x≤1} | D. | {x|-4≤x≤0且x≠-2} |
16.命题“?x∈R,f(x)<g(x)<h(x)”的否定形式是( )
| A. | ?x0∈R,f(x0)≥g(x0)≥h(x0) | B. | ?x0∈R,f(x0)≥g(x0)或g(x0)≥h(x0) | ||
| C. | ?x∈R,f(x)≥g(x)≥h(x) | D. | ?x∈R,f(x)≥g(x)或g(x)≥h(x) |
14.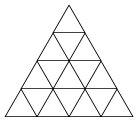 设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )
设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )
 设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )
设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{3}$ |
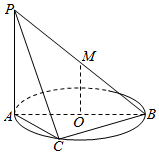 如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:
如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题: