题目内容
16.不等式log2|2+x|≤1的解集为( )| A. | {x|x≥0} | B. | {x|x≥-2} | C. | {x|0≤x≤1} | D. | {x|-4≤x≤0且x≠-2} |
分析 由对数函数的性质化对数不等式为绝对值的不等式,然后求解绝对值的不等式得答案.
解答 解:由log2|2+x|≤1,得0<|2+x|≤2,
即-2≤2+x≤2且2+x≠0,解得-4≤x≤0且x≠-2,
∴不等式log2|2+x|≤1的解集为{x|-4≤x≤0且x≠-2}.
故选:D.
点评 本题考查对数不等式和绝对值不等式的解法,关键是注意真数大于0,是中档题.

练习册系列答案
相关题目
4.设m,n是两条不同的直线,α,β是两个不同的平面( )
| A. | 若m丄n,n∥α,则m丄α | B. | 若m∥n,n丄β,则m丄β | ||
| C. | 若m∥β,β 丄a,则m丄a | D. | 若 m 丄 n,n丄β,β丄a,则 m丄 a |
2.设x>0,y>0,且2x+y=20,则lgx+lgy的最大值是( )
| A. | 50 | B. | 2 | C. | 1+lg5 | D. | 1 |
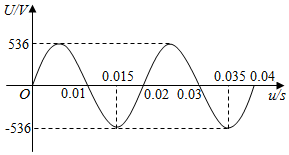 一台发电机产生地交流电的电压U和时间t之间关系的图象如图所示,由图象说出它的周期、频率和电压的最大值,并求出电压U和时间t之间的函数解析式.
一台发电机产生地交流电的电压U和时间t之间关系的图象如图所示,由图象说出它的周期、频率和电压的最大值,并求出电压U和时间t之间的函数解析式.