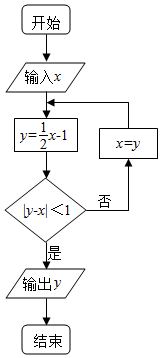
题目内容
2.已知k∈Z,$\overrightarrow{AB}$=(k,1),$\overrightarrow{CB}$=(k-2,-3),若|$\overrightarrow{AB}$|≤$\sqrt{17}$,则△ABC是直角三角形的概率是( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
分析 根据向量模长公式求出满足条件的k的个数,分类讨论,求得k的值,再根据古典概型的计算公式进行求解.
解答 解:|$\overrightarrow{AB}$|≤$\sqrt{17}$,k∈Z,知知k∈{-4,-3,-2,-1,0,1,2,3,4},由$\overrightarrow{AB}$=(k,1),$\overrightarrow{CB}$=(k-2,-3)垂直,求得k=-1,3;
$\overrightarrow{AB}$=(k,1)与$\overrightarrow{AC}=\overrightarrow{AB}-\overrightarrow{CB}$=(2,4),k=-2,
所以△ABC是直角三角形的概率是$\frac{1}{3}$,
故答案选:B.
点评 本题主要考查概率的计算,根据古典概型的概率公式,利用列举法进行求解是解决本题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.甲、乙、丙、丁和戊5名同学进行数学应用知识比赛,决出第1名至第5名(没有重复名次).已知甲、乙均未得到第1名,且乙不是最后一名,则5人的名次排列情况可能有( )
| A. | 27种 | B. | 48种 | C. | 54种 | D. | 72种 |
14.执行如图所示的程序框图,则下列说法正确的( )
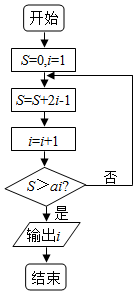

| A. | ?a∈(2,4),输出的i的值为5 | B. | ?a∈(4,5),输出的i的值为5 | ||
| C. | ?a∈(3,4),输出的i的值为5 | D. | ?a∈(2,4),输出的i的值为5 |
14.如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )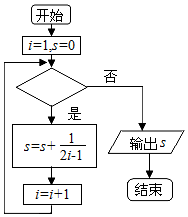

| A. | i≤1008? | B. | i>1008? | C. | i≤1009? | D. | i>1009? |
10.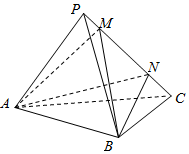 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
10.${(x-\frac{1}{{\sqrt{x}}})^6}(2{x^3}+1)$的常数项是( )
| A. | 15 | B. | 17 | C. | -15 | D. | -17 |
 如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.