题目内容
10.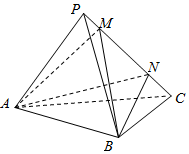 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
分析 取AC中点O,连接BO,可得BO⊥AC,再由面面垂直的性质可得BO⊥面PAC,然后利用等积法把三棱锥A-MNB的体积转化为三棱锥B-AMN得体积求解.
解答  解:如图,取AC中点O,连接BO,
解:如图,取AC中点O,连接BO,
∵AB=BC,BO⊥AC,
∵面PAC⊥面ABC,
∴由面面垂直的性质可得,BO⊥面PAC,
∵AB=BC=PA=PC=2,AC=AC,
∴△ABC≌△APC,
又AB⊥BC,
∴AP⊥PC,即△APC为直角三角形,
在Rt△ABC中,由AB=BC=2,得AC=$2\sqrt{2}$,
∴OB=$\sqrt{2}$,
则VA-MNB=VB-AMN,
又MN=$\sqrt{2}$,
∴VA-MNB=VB-AMN=$\frac{1}{3}×\frac{1}{2}×2×\sqrt{2}×\sqrt{2}=\frac{2}{3}$.
故选:A.
点评 本题考查棱柱、棱锥、棱台体积的求法,考查空间想象能力和思维能力,训练了利用等积法求多面的体积,是中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
2.执行如图所示的程序框图,输出的S值为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.已知k∈Z,$\overrightarrow{AB}$=(k,1),$\overrightarrow{CB}$=(k-2,-3),若|$\overrightarrow{AB}$|≤$\sqrt{17}$,则△ABC是直角三角形的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
6.已知焦点在x轴双曲线的一条渐近线的倾斜角$\frac{π}{6}$,则此双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |

