题目内容
13.甲、乙、丙、丁和戊5名同学进行数学应用知识比赛,决出第1名至第5名(没有重复名次).已知甲、乙均未得到第1名,且乙不是最后一名,则5人的名次排列情况可能有( )| A. | 27种 | B. | 48种 | C. | 54种 | D. | 72种 |
分析 由题意可知,第一名从丙、丁和戊中产生,最后一名从甲和(丙、丁和戊其中2名)产生,其它名次任意排,根据分步计数原理可得.
解答 解:由题意可知,第一名从丙、丁和戊中产生,最后一名从甲和(丙、丁和戊其中2名)产生,其它名次任意排,故有A31A31A33=54种,
故选:C.
点评 本题考查了分步计数原理,特殊元素优先安排,属于基础题.

练习册系列答案
相关题目
2.执行如图所示的程序框图,输出的S值为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.已知k∈Z,$\overrightarrow{AB}$=(k,1),$\overrightarrow{CB}$=(k-2,-3),若|$\overrightarrow{AB}$|≤$\sqrt{17}$,则△ABC是直角三角形的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
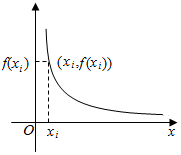 已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n).
已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n). 为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.
为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.