题目内容
已知函数 对任意实数
对任意实数 恒有
恒有 且当
且当 时,有
时,有 且
且 .
.
(1)判断 的奇偶性;
的奇偶性;
(2)求 在区间
在区间 上的最大值;
上的最大值;
(3)解关于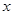 的不等式
的不等式 .
.
(1)奇函数;(2) ;
;
(3) 当
当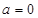 时,
时,
当 时,
时,
当 时,
时,
当 时,
时, 
解析试题分析:(1)赋值法:先令 ,再令
,再令
(2)根据 以及当
以及当 时,有
时,有 ,利用函数单调性的定义判断得出
,利用函数单调性的定义判断得出 为
为 上的减函数;并由单调性求其最值;
上的减函数;并由单调性求其最值;
(3)由(1)和(2)的结论,先将不等式 化为
化为 ;再由函数的单调性转化为 关于
;再由函数的单调性转化为 关于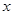 的不等式
的不等式 对
对 的不同取值,分别讨论不等式的解.
的不同取值,分别讨论不等式的解.
试题解析:解(1)取 则
则
取
 对任意
对任意 恒成立 ∴
恒成立 ∴ 为奇函数.
为奇函数.
(2)任取 , 则
, 则

 又
又 为奇函数
为奇函数 
∴ 在(-∞,+∞)上是减函数.
在(-∞,+∞)上是减函数. 对任意
对任意 ,恒有
,恒有
而
 ∴
∴ 在[-3,3]上的最大值为6
在[-3,3]上的最大值为6
(3)∵ 为奇函数,∴整理原式得
为奇函数,∴整理原式得 
进一步可得
而 在(-∞,+∞)上是减函数,
在(-∞,+∞)上是减函数,

 当
当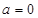 时,
时,
当 时,
时,
当 时,
时,
当 时,
时, 
考点:1、赋值法解决抽象函数的有关问题;2、函数单调性的定义;3、分类讨论的思想.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 且
且 ,求函数
,求函数 的单调区间.
的单调区间. ,若函数
,若函数 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数 的取值范围.
的取值范围.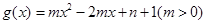 在区间
在区间  上有最大值
上有最大值 ,最小值
,最小值 .
. 的解析式;
的解析式; .若
.若 在
在 时恒成立,求
时恒成立,求 的取值范围.
的取值范围. 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有 ,且当
,且当 时,
时, 。
。 是否满足这些条件;
是否满足这些条件; ,求方程
,求方程 的解。
的解。 ;
; ;
; ,
,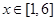 ,
, .
. ,试判断并证明函数
,试判断并证明函数 的单调性;
的单调性;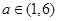 时,求函数
时,求函数 .
. 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.