题目内容
已知二次函数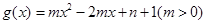 在区间
在区间  上有最大值
上有最大值 ,最小值
,最小值 .
.
(1)求函数 的解析式;
的解析式;
(2)设 .若
.若 在
在 时恒成立,求
时恒成立,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据二次函数的最值建立方程组,即可求函数 的解析式;(2)将
的解析式;(2)将 在
在 时恒成立进行转化为求函数最值,即可求出
时恒成立进行转化为求函数最值,即可求出 的取值范围.求最值时考虑利用换元当将函数转化为求二次函数在一个闭区间上的最值.
的取值范围.求最值时考虑利用换元当将函数转化为求二次函数在一个闭区间上的最值.
试题解析:(1)∵ ,
,
∴函数 的图象的对称轴方程为
的图象的对称轴方程为 .
. 依题意得
依题意得 ,即
,即 ,解得
,解得 ,
,
∴ .
.
(2)∵ ,∴
,∴ .
.
∵ 在
在 时恒成立,即
时恒成立,即 在
在 时恒成立,
时恒成立,
∴ 在
在 时恒成立,
时恒成立,
只需  .
.
令 ,由
,由 得
得
设
 ,
,
∵ ,
,
∴函数 的图象的对称轴方程为
的图象的对称轴方程为 .
.
当 时,取得最大值
时,取得最大值 .
.
∴ ∴
∴ 的取值范围为
的取值范围为 .
.
考点:1、函数恒成立问题;2、函数解析式的求解及常用方法;3、二次函数在闭区间上的最值.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
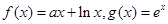 .
.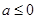 时,求
时,求 的单调区间;
的单调区间;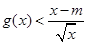 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;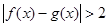 .
.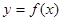 的定义域为
的定义域为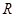 ,若存在常数
,若存在常数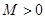 ,使得
,使得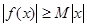 对一切实数
对一切实数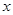 均成立,则称
均成立,则称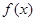 为“圆锥托底型”函数.
为“圆锥托底型”函数.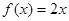 ,
,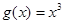 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.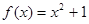 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出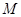 的最大值.
的最大值.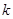 、
、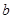 满足什么条件,
满足什么条件,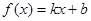 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.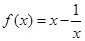 ,
,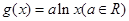 .
.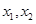 ,其中
,其中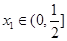 ,求
,求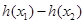 的最小值.
的最小值.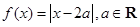 .
.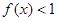 的解集为
的解集为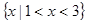 ,求
,求 的值;
的值;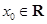 ,使
,使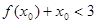 ,求
,求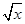 +2)=x+4
+2)=x+4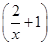 =lgx,求f(x);
=lgx,求f(x);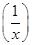 =2x,x∈R且x≠0,求f(x);
=2x,x∈R且x≠0,求f(x); 对任意实数
对任意实数 恒有
恒有 且当
且当 时,有
时,有 且
且 .
. 上的最大值;
上的最大值;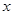 的不等式
的不等式 .
. 是奇函数.
是奇函数.