题目内容
已知函数 ,
,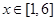 ,
, .
.
(1)若 ,试判断并证明函数
,试判断并证明函数 的单调性;
的单调性;
(2)当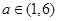 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式 .
.
(1)当 时,
时, 在
在 上是增函数,证明过程详见试题解析; (2)函数
上是增函数,证明过程详见试题解析; (2)函数 的最大值的表达式
的最大值的表达式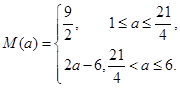 .
.
解析试题分析:(1)当 时,
时, ,用单调性的定义即可证明函数式单调递增的;
,用单调性的定义即可证明函数式单调递增的;
(2)当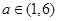 时,
时, ; 分
; 分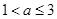 和
和 两种情况分别求出各段的最大值即可.
两种情况分别求出各段的最大值即可.
试题解析:(1)判断:若 ,函数
,函数 在
在 上是增函数. 1分
上是增函数. 1分
证明:当 时,
时, ,
,
在区间 上任意
上任意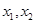 ,设
,设 ,
,
所以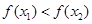 ,即
,即 在
在 上是增函数. 5分
上是增函数. 5分
(注:用导数法证明或其它方法说明也同样给5分)
(2)因为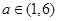 ,所以
,所以 7分
7分
①当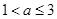 时,
时, 在
在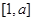 上是增函数,在
上是增函数,在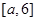 上也是增函数,
上也是增函数,
所以当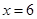 时,
时, 取得最大值为
取得最大值为 ; 9分
; 9分
②当 时,
时, 在
在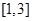 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,
在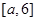 上是增函数, 11分
上是增函数, 11分
而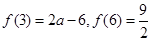 ,
,
当 时,
时,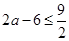 ,当
,当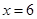 时,函数
时,函数 取最大值为
取最大值为 ;
;
当 时,
时,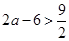 ,当
,当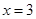 时,函数
时,函数 取最大值为
取最大值为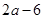 ;13分
;13分
综上得,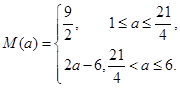 15分
15分
考点:函数的性质、函数最值的求法、分类讨论思想.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 对任意实数
对任意实数 恒有
恒有 且当
且当 时,有
时,有 且
且 .
. 上的最大值;
上的最大值; 的不等式
的不等式 .
.
 的单调性,并证明;
的单调性,并证明; 是奇函数.
是奇函数. ,其中
,其中 是常数.
是常数. 时,
时,  是奇函数;
是奇函数; 时,
时,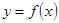 的图像上不存在两点
的图像上不存在两点 、
、 ,使得直线
,使得直线 平行于
平行于 轴.
轴.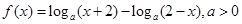 且
且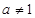 .
. 的定义域;
的定义域; ,函数
,函数 .
.
 时,画出函数
时,画出函数 的大致图像;
的大致图像; 解的个数.
解的个数. .
.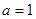 时,函数
时,函数 的图像在点
的图像在点 处的切线方程;
处的切线方程; 时,解不等式
时,解不等式 ;
;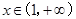 ,直线
,直线 的图像下方.求整数
的图像下方.求整数 的最大值.
的最大值.