题目内容
3.对于平面α和两条直线m,n,下列命题中真命题是( )| A. | 若m⊥α,m⊥n,则n∥α | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m,n与α所成的角相等,则m∥n | D. | 若m?α,m∥n,且n在平面α外,则n∥α |
分析 在A中,n∥α或n?α;在B中,m与n相交、平行或异面;在C中,m与n相交、平行或异面;在D中,由直线与平面平行的判定定理得n∥α.
解答 解:在A中:若m⊥α,m⊥n,则n∥α或n?α,故A错误;
在B中:若m∥α,n∥α,则m与n相交、平行或异面,故B错误;
在C中:若m,n与α所成的角相等,则m与n相交、平行或异面,故C错误;
在D中:若m?α,m∥n,且n在平面α外,则由直线与平面平行的判定定理得n∥α,故D正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列函数f(x)中,满足“对任意x1、x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
| A. | f(x)=(x-1)2 | B. | f(x)=ex | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=ln(x+1) |
15.$\frac{{2{{sin}^2}55°-1}}{sin20°}$的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -1 | D. | 1 |
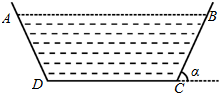 2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?
2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?