题目内容
12.已知菱形ABCD的边长为4,∠ABC=120°,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率$1-\frac{{\sqrt{3}π}}{24}$.分析 以菱形ABCD的各个顶点为圆心、半径为1作圆如图所示,可得当该点位于图中阴影部分区域时,它到四个顶点的距离均大于1.因此算出菱形ABCD的面积和阴影部分区域的面积,利用几何概型计算公式加以计算,即可得到所求的概率.
解答 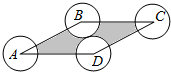 解:分别以菱形ABCD的各个顶点为圆心,作半径为1的圆,如图所示.
解:分别以菱形ABCD的各个顶点为圆心,作半径为1的圆,如图所示.
在菱形ABCD内任取一点P,则点P位于四个圆的外部时,
满足点P到四个顶点的距离均大于1,即图中的阴影部分区域
∵S菱形ABCD=AB•BCsin120°=4×4×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$,
∴S阴影=S菱形ABCD-S空白=8$\sqrt{3}$-π×12=8$\sqrt{3}$-π.
因此,该点到四个顶点的距离大于1的概率P=$\frac{{S}_{阴影}}{{S}_{菱形}}$=$1-\frac{{\sqrt{3}π}}{24}$,
故答案为:$1-\frac{{\sqrt{3}π}}{24}$.
点评 本题主要考查几何概型的概率的计算,根据对应分别求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
3.对于平面α和两条直线m,n,下列命题中真命题是( )
| A. | 若m⊥α,m⊥n,则n∥α | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m,n与α所成的角相等,则m∥n | D. | 若m?α,m∥n,且n在平面α外,则n∥α |
1.已知一个算法,其流程图如图所示,则输出结果是( )


| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
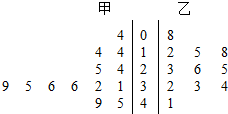 现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.
现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.