题目内容
15．$\frac{{2{{sin}^2}55°-1}}{sin20°}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | -1 | D． | 1 |
分析 有条阿金利用二倍角的余弦公式、诱导公式求得要求式子的值．
解答 解：$\frac{{2{{sin}^2}55°-1}}{sin20°}$=$\frac{-cos110°}{sin20°}$=$\frac{sin20°}{sin20°}$=1，
故选：D．
点评 本题主要考查二倍角的余弦公式、诱导公式的应用，属于基础题．
练习册系列答案
相关题目
5．若全集U=R，集合A={x|x2+4x+3＞0}，B={x|log3（2-x）≤1}，则∁U（A∩B）=（ ）
| A． | {x|x＜-1或x＞2} | B． | {x|x＜-1或x≥2} | C． | {x|x≤-1或x＞2} | D． | {x|x≤-1或x≥2} |
3．对于平面α和两条直线m，n，下列命题中真命题是（ ）
| A． | 若m⊥α，m⊥n，则n∥α | B． | 若m∥α，n∥α，则m∥n | ||
| C． | 若m，n与α所成的角相等，则m∥n | D． | 若m?α，m∥n，且n在平面α外，则n∥α |
10．α是第四象限角，$tanα=-\frac{4}{3}$，则sinα等于（ ）
| A． | $\frac{4}{5}$ | B． | $-\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $-\frac{3}{5}$ |
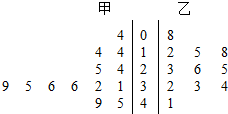现今社会对食品安全的高度重视，各级政府加强了对食品安全的检查力度．某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查．如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图，则甲、乙两个检查组每天检查到的食品种数的中位数的和是58．
5．已知a、b、c表示不同的直线，α、β、γ表示不同的平面，则下列判断正确的是（ ）
| A． | 若a⊥c，b⊥c，则a∥b | B． | 若α⊥γ，β⊥γ，则α∥β | C． | 若α⊥a，β⊥a，则α∥β | D． | 若a⊥α，b⊥a，则b∥α |