题目内容
9.(1)求曲线f(x)=$\frac{2}{x}$在点(-2,-1)处的切线方程;(2)求经过点(2,0)且与曲线y=$\frac{1}{x}$相切的直线方程.
分析 (1)求出导数,求得切线的斜率,由点斜式方程即可得到所求方程;
(2)设出切点(m,n),求得导数,求得切线的斜率,由两点的斜率公式可得m=1,再由点斜式方程即可得到所求方程.
解答 解:(1)f(x)=$\frac{2}{x}$的导数为f′(x)=-$\frac{2}{{x}^{2}}$,
在点(-2,-1)处的切线斜率为k=-$\frac{1}{2}$,
可得在点(-2,-1)处的切线方程为y+1=-$\frac{1}{2}$(x+2),即为y=-$\frac{1}{2}$x-2;
(2)设切点为(m,n),
由y=$\frac{1}{x}$的导数为y′=-$\frac{1}{{x}^{2}}$,
可得切线的斜率为k=-$\frac{1}{{m}^{2}}$,
由题意可得-$\frac{1}{{m}^{2}}$=$\frac{n}{m-2}$=$\frac{1}{{m}^{2}-2m}$,
解得m=1(0舍去),
即有相切的直线方程为y-0=-(x-2),即为y=-x+2.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和确定切点是解题的关键,属于基础题.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
20.过点M(5,-2),且在x轴、y轴上截距互为相反数的直线方程为( )
| A. | x+y-3=0 | B. | x+y-3=0或2x+5y=0 | ||
| C. | x-y-7=0或2x+5y=0 | D. | x-y-7=0或x+y-3=0 |
14.在区间(-1,+∞)内,函数y=ex-x是( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减 | D. | 先减后增 |
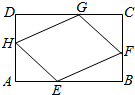 如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.
如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y. ,则
,则 为( )
为( )


