题目内容
4.求函数f(x)=$\sqrt{2sinx+1}$+lg(5-x)-lg(5+x)的定义域.分析 根据函数f(x)的解析式,列出使解析式有意义的不等式组$\left\{\begin{array}{l}{2sinx+1≥0}\\{5-x>0}\\{5+x>0}\end{array}\right.$,求出解集即可.
解答 解:∵函数f(x)=$\sqrt{2sinx+1}$+lg(5-x)-lg(5+x),
∴$\left\{\begin{array}{l}{2sinx+1≥0}\\{5-x>0}\\{5+x>0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{sinx≥-\frac{1}{2}}\\{-5<x<5}\end{array}\right.$,
即$\left\{\begin{array}{l}{-\frac{π}{6}+2kπ≤x≤\frac{7π}{6}+2kπ,k∈Z}\\{-5<x<5}\end{array}\right.$,
即-5<x≤-$\frac{5π}{6}$或-$\frac{π}{6}$≤x≤$\frac{7π}{6}$;
∴f(x)的定义域是(-5,-$\frac{5π}{6}$]∪[-$\frac{π}{6}$,$\frac{7π}{6}$].
点评 本题考查了利用函数解析式求定义域的应用问题,是基础题目.

练习册系列答案
相关题目
14.下列函数是偶函数的是( )
| A. | y=x3 | B. | y=2x2-3 | C. | y=x | D. | y=x2,x∈[0,1] |
15.“a<-3”是“f(x)=ax+3在区间(-1,2)上存在零点x0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
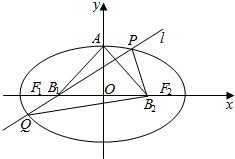 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.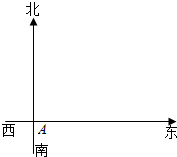 一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.
一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地. 分别为正方形
分别为正方形 的边
的边 和
和 的中点,则
的中点,则 ( )
( ) B.
B. C.
C. D.
D.