题目内容
15.某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如表:| 月平均气温x(℃) | 17 | 13 | 8 | 2 |
| 月销售量y(件) | 34 | 43 | 50 | 65 |
(2)气象部门预测下个月的平均气温约为3℃,据此估计,求该商场下个月毛衣的销售量.
(参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$)
分析 (1)分别求出样本的中心点,求出方程的系数$\widehat{b}$,$\widehat{a}$的值,求出回归方程即可;(2)将x=3代入方程求出函数的预报值即可.
解答 解:(1)$\overline{x}=(17+13+8+2)÷4=10$,$\overline{y}=(34+43+50+65)÷4=48$,
$\sum_{i=1}^4{{x_i}{y_i}}=17×34+13×43+8×50+2×65=1667$,$\sum_{i=1}^4{x_i^2}=526$,
$\widehat{b}$=$\frac{1667-4×10×48}{{526-4×{{10}^2}}}=-2.01≈-2.0$,$a=\bar y-b\overline{x}=48-(-2.01)×10≈68.1$,
∴线性回归方程为$\widehat{y}$=-2.0x+68,1;
(2)气象部门预测下个月的平均气温约为3℃,
据此估计,该商场下个月毛衣的销售量为:
$\widehat{y}$=-2.0x+68.1=-2.0×3+68.1≈62(件)
点评 本题考查了求回归方程问题,考查函数求值问题,是一道基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5.函数f(x)=x3-3ax2+(2a+1)x既有极小值又有极大值,则a的取值范围为( )
| A. | -$\frac{1}{3}$<a<1 | B. | a>1或a$<-\frac{1}{3}$ | C. | -1$<a<\frac{1}{3}$ | D. | a$>\frac{1}{3}$或a<-1 |
6.如图,小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )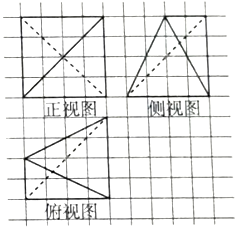

| A. | 8$\sqrt{3}$ | B. | $\frac{80}{3}$ | C. | 16$\sqrt{3}$ | D. | 32 |
7.设X是一个离散型随机变量,则下列不能成为X的概率分布列的一组数据是( )
| A. | 0,$\frac{1}{2}$,0,0,$\frac{1}{2}$ | B. | 0.1,0.2,0.3,0.4 | ||
| C. | p,1-p(0≤p≤1) | D. | $\frac{1}{1×2}$,$\frac{1}{2×3}$,…,$\frac{1}{7×8}$ |
4.如图为体积是3的几何体的三视图,则正视图的x值是( )
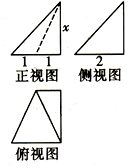

| A. | 2 | B. | $\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |