题目内容
12.数学与自然、生活相伴相随,无论是蜂的繁殖规律,树的分枝,还是钢琴音阶的排列,当中都蕴含了一个美丽的数学模型Fibonacci(斐波那契数列):1,1,2,3,5,8,13,21…,这个数列前两项都是1,从第三项起,每一项都等于前面两项之和,请你结合斐波那契数列,尝试解答下面的问题:小明走楼梯,该楼梯一共8级台阶,小明每步可以上一级或二级,请问小明的不同走法种数是( )| A. | 20 | B. | 34 | C. | 42 | D. | 55 |
分析 从第1级开始递推,脚落到第1级只有从地上1种走法;第二级有两种可能,从地跨过第一级或从第一级直接迈上去;登上第3级,分两类,要么从第1级迈上来,要么从第2级迈上来,所以方法数是前两级的方法和;依此类推,以后的每一级的方法数都是前两级方法的和;直到8级,每一级的方法数都求出,因此得解.
解答 解:递推:
登上第1级:1种
登上第2级:2种
登上第3级:1+2=3种(前一步要么从第1级迈上来,要么从第2级迈上来)
登上第4级:2+3=5种(前一步要么从第2级迈上来,要么从第3级迈上来)
登上第5级:3+5=8种
登上第6级:5+8=13种
登上第7级:8+13=21种
登上第8级:13+21=34种,
故选B.
点评 本题考查了裴波那切数列的灵活应用,关键是先找到规律,然后递推出大数的情况.

练习册系列答案
相关题目
2.已知α为第四象限角,$sinα+cosα=\frac{1}{5}$,则$tan\frac{α}{2}$的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
17.已知集合 A={x|x2-x-2>0},B={x|1≤x≤3},则图中阴影部分所表示的集合为( )
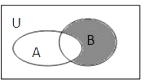

| A. | [1,2) | B. | (1,3] | C. | [1,2] | D. | (2,3] |