题目内容
20.已知函数$\begin{array}{l}f(x)=\left\{\begin{array}{l}{e^x}-1,({x<1})\\{x^3}-9{x^2}+24x-16,({x≥1})\end{array}\right.\end{array}$,则关于x的方程|f(x)|=a(a为实数)根个数不可能为( )| A. | 1 | B. | 3 | C. | 5 | D. | 6 |
分析 判断f(x)的单调性,计算f(x)的极值,作出y=|f(x)|的函数图象,根据函数图象得出方程|f(x)|=a的解的情况.
解答 解:当x<1时,f(x)为增函数,且f(0)=0,
当x≥1时,f′(x)=3x2-18x+24,
令f′(x)=0得3x2-18x+24=0,解得x1=2,x2=4,
当1≤x<2时,f′(x)>0,当2<x<4时,f′(x)<0,当x>4时,f′(x)>0,
∴当x=2时,f(x)取得极大值f(2)=4,当x=4时,f(x)取得极小值f(4)=0,
做出y=f(x)的函数图象如图:
将x轴下方的图象向上翻折得出y=|f(x)|的函数图象如图所示: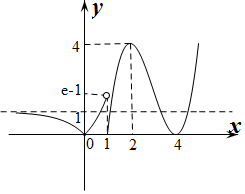
由图象可知:
当a<0时,|f(x)|=a无解,
当a=0时,|f(x)|=a有3解,
当0<a<1时,|f(x)|=a有5解,
当1≤a<e-1时,|f(x)|=a有4解,
当e-1≤a<4时,|f(x)|=a有3解,
当a=4时,|f(x)|=a有2解,
当a>4时,|f(x)|=a有1解.
故选D.
点评 本题考查了函数单调性的判断,函数零点的个数与函数图象的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在锐角三角形ABC 中,角 A,B,C 的对边分别为 a,b,c.若a=2bsinC,则tanA+tanB+tanC的最小值是( )
| A. | 4 | B. | $3\sqrt{3}$ | C. | 8 | D. | $6\sqrt{3}$ |
11.已知当x<1时,f(x)=(2-a)x+1;当x≥1时,f(x)=ax(a>0且a≠1).若对任意x1≠x2,都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$成立,则a的取值范围是( )
| A. | (1,2) | B. | $(1,\frac{3}{2}]$ | C. | $[\frac{3}{2},2)$ | D. | (0,1)∪(2,+∞) |
8.已知全集U=R,集合$A=\left\{{x|{2^x}>\frac{1}{2}}\right\},B=\left\{{x|{{log}_3}x<1}\right\}$,则A∩(∁UB)=( )
| A. | (-1,+∞) | B. | [3,+∞) | C. | (-1,0)∪(3,+∞) | D. | (-1,0]∪[3,+∞) |
15.下列命题中真命题是( )
| A. | $?x∈({-∞,\frac{π}{4}}),tanx≤1$ | |
| B. | 设l,m表示不同的直线,α表示平面,若m∥l且m⊥α,则l∥α | |
| C. | 利用计算机产生0和l之间的均匀随机数m,则事件“3m-1≥0”发生的概率为$\frac{1}{3}$ | |
| D. | “a>0,b>0”是“$\frac{b}{a}+\frac{a}{b}$≥2”的充分不必要条件 |
5.i为虚数单位,复数$\frac{3+i}{1-i}$的虚部是( )
| A. | 2i | B. | 2 | C. | -2i | D. | -1 |
9.从六个数1,3,4,6,7,9中任取2个数,则这两个数的平均数恰好是5的概率为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
10.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 24 | B. | 48 | C. | 54 | D. | 72 |