题目内容
4.在△ABC中,∠ACB=120°,D是 AB 上一点,满足∠ADC=60°,CD=2,若CB$≥\sqrt{6}$,则∠ACD的最大值为105°.分析 如图所示,过C作CE⊥AB,垂足为E.在Rt△CED中,可得CE=$\sqrt{3}$,∠ECD=30°.在Rt△CEB中,由CB$≥\sqrt{6}$,可得cos∠BCE=$\frac{CE}{CB}$≤$\frac{\sqrt{2}}{2}$,即可得出.
解答 解:如图所示,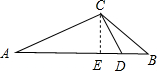 过C作CE⊥AB,垂足为E.
过C作CE⊥AB,垂足为E.
在Rt△CED中,∠ADC=60°,CD=2,
∴CE=2sin60°=$\sqrt{3}$,∠ECD=30°.
在Rt△CEB中,∵CB$≥\sqrt{6}$,
则cos∠BCE=$\frac{CE}{CB}$≤$\frac{\sqrt{3}}{\sqrt{6}}$=$\frac{\sqrt{2}}{2}$,
∴90°>∠BCE≥45°.
∴∠BCD≥15°,
∴∠ACD≤120°-15°=105°.
故答案为:105°.
点评 本题考查了直角三角形的边角关系、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y-1≤0}\\{x+y≥0}\\{x+2y-4≥0}\end{array}\right.$,则z=x-2y的最大值为( )
| A. | -12 | B. | -1 | C. | 0 | D. | $\frac{3}{2}$ |
15.下列命题中真命题是( )
| A. | $?x∈({-∞,\frac{π}{4}}),tanx≤1$ | |
| B. | 设l,m表示不同的直线,α表示平面,若m∥l且m⊥α,则l∥α | |
| C. | 利用计算机产生0和l之间的均匀随机数m,则事件“3m-1≥0”发生的概率为$\frac{1}{3}$ | |
| D. | “a>0,b>0”是“$\frac{b}{a}+\frac{a}{b}$≥2”的充分不必要条件 |
19.《九章算术•均输》中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5 钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,乙所得为( )
| A. | $\frac{4}{3}$钱 | B. | $\frac{5}{4}$钱 | C. | $\frac{6}{5}$钱 | D. | $\frac{7}{6}$钱 |
9.从六个数1,3,4,6,7,9中任取2个数,则这两个数的平均数恰好是5的概率为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
16.执行如图所示的程序框图,输出的S值为( )


| A. | 3025 | B. | -3024 | C. | -3025 | D. | -6050 |
14.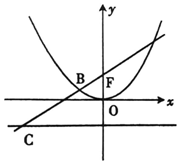 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )
 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2-$\sqrt{2}$ |