题目内容

18．若数列{an}满足an+a${\;}_{n+1}=4n+2（n≥1，n∈{N}^{+}）$，且a1=x，{an}单调递增，则x的取值范围是（1，3）．

分析 数列{an}单调递增?a1＜a2＜a3，解出即可得出．

解答 解：数列{an}单调递增?a1＜a2＜a3，
∵数列{an}满足an+a${\;}_{n+1}=4n+2（n≥1，n∈{N}^{+}）$，且a1=x，
解得a2=6-x，a3=4+x．
∴x＜6-x＜4+x，
解得1＜x＜3．
故答案为：（1，3）．

点评 本题考查了不等式的解法、数列的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
8．如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠BCD=120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF=1
（Ⅰ）求证：AD⊥平面BFED；
（Ⅱ）点P是线段EF上运动，且$\frac{EP}{PF}$=2，求三棱锥E-APD的体积．
9．若随机变量X～N（μ，σ2），且P（X＞5）=P（X＜-1）=0.2，则P（2＜X＜5）=0.3．
6．设向量$\overrightarrow{{a}_{n}}$=（cos$\frac{nπ}{6}$，sin$\frac{nπ}{6}$+cos$\frac{nπ}{6}$），数列{bn}满足bn=$\overrightarrow{{a}_{n-1}}$•$\overrightarrow{{a}_{n}}$．求b1+b2+b3+…+b12的值．
13．已知函数f（x）=|$\frac{e}{x}$-lnx|，g（x）=|e1-x+lnx+a|
（1）将f（x）写成分段函数的形式（不用说明理由），并求f（x）的单调区间．
（2）若x≥1且-1-e1-x＜a＜-1，比较f（x）与g（x）的大小．
3．一个箱中原来装有大小相同的5个小球，其中3个红球，2个白球．规定：进行一次操作是指“从箱中随机取出一个球，如果取出的是红球，则把它放回箱中；如果取出的是白球，则该球不放回，并另补一个红球到箱中”．
（1）求进行第二次操作后，箱中红球个数为4的概率．
（2）求进行第二次操作后，箱中红球个数ξ的分布列．
10．执行如图的程序框图，则输出的i=4．
7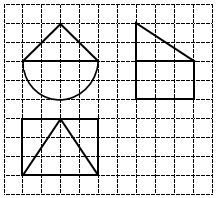．如图，网格纸上的小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积是（　　）
A．4+6πB．8+6πC．4+12πD．8+12π
8．已知a＞0，b＞0，且$\frac{2}{2+a}+\frac{1}{a+2b}=1$，则a+b的最小值是$\sqrt{2}+\frac{1}{2}$此时a=$\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网