题目内容
8. 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1(Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)点P是线段EF上运动,且$\frac{EP}{PF}$=2,求三棱锥E-APD的体积.
分析 (1)根据平面几何知识计算AB,BD,根据勾股定理的逆定理得出AD⊥BD,由平面BFED⊥平面ABCD得出AD⊥平面BFED;
(2)以△PDE为棱锥的底面,则AD为棱锥的高,代入棱锥的体积公式计算.
解答 (1)证明:在梯形ABCD中,
∵AB∥CD,AD=DC=CB=1,∠BCD=120°,
∴AB=2.∴BD2=BC2+CD2-2BC•CD•cos120°=3.
∴AB2=AD2+BD2,∴AD⊥BD.
∵平面BFED⊥平面ABCD,平面BFED∩平面ABCD=BD,AD?平面ABCD,DE⊥DB,
∴AD⊥平面BFED.
(2)∵四边形BFED为矩形,∴EF=BD=$\sqrt{3}$,DE=BF=1,
∵$\frac{EP}{PF}$=2,∴$PE=\frac{{2\sqrt{3}}}{3}$.
∴S△PDE=$\frac{1}{2}PE•DE$=$\frac{1}{2}×\frac{2\sqrt{3}}{3}×1=\frac{\sqrt{3}}{3}$,
∴VE-APD=VA-PDE=$\frac{1}{3}{S}_{△PDE}•DE$=$\frac{1}{3}×\frac{\sqrt{3}}{3}×1$=$\frac{\sqrt{3}}{9}$.
点评 本题考查了线面垂直的判定,面面垂直的性质,棱锥的体积计算,选择恰当的底面和高是计算体积的关键.

练习册系列答案
相关题目
19.从集合A={-3,-2,-1,2}中随机选取一个数记为k,从集合B={-2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第四象限的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
3.设函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤1}\\{lo{g}_{2}x,x>1}\end{array}\right.$,若f(a)>1,则a的取值范围是( )
| A. | (-∞,1)∪(2,+∞) | B. | (0,+∞) | C. | (2,+∞) | D. | (-∞,0)∪(2,+∞) |
20.设f(x)是定义在R上的函数,对x∈R都有f(-x)=f(x),f(2+x)=f(2-x),且当x∈[-2,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\root{3}{4}$) | D. | ($\root{3}{4}$,2) |
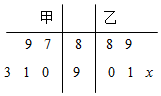 如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.