题目内容
1.等比数列{an}中各项均为正数,Sn是其前n项和,且满足2S3=8a1+3a2,a4=16,则S4=30.分析 利用等比数列的通项公式与求和公式即可得出.
解答 解:设等比数列{an}的公比为q>0,∵2S3=8a1+3a2,a4=16,
∴2a1(1+q+q2)=a1(8+3q),${a}_{1}{q}^{3}$=16,
解得a1=q=2.
则S4=$\frac{2({2}^{4}-1)}{2-1}$=30.
故答案为:30.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知集合A={x|x2-2x-3<0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-2<x<2} | B. | {x|-2<x<3} | C. | {x|-1<x<3} | D. | {x|-1<x<2} |
6.设复数z=-2+i(i是虚数单位),z的共轭复数为$\overline{z}$,则|(2+z)•$\overline{z}$|等于( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{10}$ |
11.已知点F1,F2分别是双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右两焦点,过点F1的直线l与双曲线的左右两支分别交于P,Q两点,若△PQF2是以∠PQF2为顶角的等腰三角形,其中$∠PQ{F_2}∈[\frac{π}{3},π)$,则双曲线离心率e
的取值范围为( )
的取值范围为( )
| A. | $[\sqrt{7},3)$ | B. | $[1,\sqrt{7})$ | C. | $[\sqrt{5},3)$ | D. | $[\sqrt{5},\sqrt{7})$ |
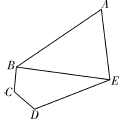 某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.
某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.