题目内容
10.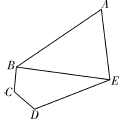 某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.
某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.(1)求道路BE的长度;
(2)求生活区△ABE面积的最大值.
分析 (1)连接BD,在△BCD中,由余弦定理得:BD,在Rt△BDE中,求解BE即可.
(2)设∠ABE=α,在△ABE中,由正弦定理,求解AB,AE,表示S△ABE,然后求解最大值.
解答 解:(1)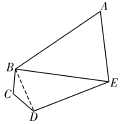
如图,连接BD,在△BCD中,由余弦定理得:$B{D^2}=B{C^2}+C{D^2}-2BC•CDcos∠BCD=\frac{27}{100}$,
∴$BD=\frac{{3\sqrt{3}}}{10}$.
∵BC=CD,∴$∠CDB=∠CBD=\frac{{π-\frac{2}{3}π}}{2}=\frac{π}{6}$,
又$∠CDE=\frac{2π}{3}$,∴$∠BDE=\frac{π}{2}$.
在Rt△BDE中,所以$BE=\sqrt{B{D^2}+D{E^2}}=\sqrt{{{({\frac{{3\sqrt{3}}}{10}})}^2}+{{({\frac{9}{10}})}^2}}=\frac{{3\sqrt{3}}}{5}$.
(2)设∠ABE=α,∵$∠BAE=\frac{π}{3}$,∴$∠AEB=\frac{2π}{3}-α$.
在△ABE中,由正弦定理,得$\frac{AB}{sin∠AEB}=\frac{AE}{sin∠ABE}=\frac{BE}{sin∠BAE}=\frac{{3\sqrt{3}}}{{5sin\frac{π}{3}}}=\frac{6}{5}$,
∴$AB=\frac{6}{5}sin({\frac{2π}{3}-α}),AE=\frac{6}{5}sinα$.
∴${S_{△ABE}}=\frac{1}{2}|{AB}||{AE}|sin\frac{π}{3}=\frac{{9\sqrt{3}}}{25}[{sin({\frac{2π}{3}-α})sinα}]$
=$\frac{{9\sqrt{3}}}{25}[{\frac{1}{2}sin({2α-\frac{π}{6}})+\frac{1}{4}}]≤\frac{{9\sqrt{3}}}{25}({\frac{1}{2}+\frac{1}{4}})=\frac{{27\sqrt{3}}}{100}$.
∵$0<α<\frac{2π}{3}$,∴$\frac{π}{6}<α+\frac{π}{6}<\frac{5π}{6}$.
∴当$2α-\frac{π}{6}=\frac{π}{2}$,即$α=\frac{π}{3}$时,S△ABE取得最大值为$\frac{{27\sqrt{3}}}{100}$,
即生活区△ABE面积的最大值为$\frac{{27\sqrt{3}}}{100}k{m^2}$.
注:第(2)问也可用余弦定理和均值不等式求解.
点评 本题考查余弦定理以及正弦定理的应用,考查距离的求法,是中档题.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | $\frac{1}{e}$ | B. | 1-$\frac{1}{e}$ | C. | $\frac{e}{1+e}$ | D. | $\frac{1}{1+e}$ |
| A. | $[\sqrt{5},2\sqrt{5}]$ | B. | $[\sqrt{5},2\sqrt{10})$ | C. | $(\sqrt{5},\sqrt{10})$ | D. | $[\sqrt{5},2\sqrt{10}]$ |
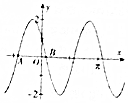 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | B. | [$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{6}$+2kπ,$\frac{π}{3}$+2kπ](k∈Z) | D. | [$\frac{π}{3}$+2kπ,$\frac{5π}{6}$+2kπ](k∈Z) |