题目内容
已知函数f(n)=
,设an=f(n)+f(n+1),则数列{an}前100项之和为( )
|
| A、0 | B、100 |
| C、-100 | D、200 |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:本题可以根据函数f(n)=
,找到f(n)的取值的规律,再利用条件an=f(n)+f(n+1),写出数列{an}的特征,利用错位相减法,求出数列{an}前100项之和,得到本题结论.
|
解答:
解:∵函数f(n)=
,
∴n∈N*,f(n)的值依次为:12,-22,32,-42,52,-62,72,-82,…
∵an=f(n)+f(n+1),
∴a1=12-22=-1-2,a2=-22+32=2+3,a3=32-42=-3-4,a4=-42+52=4+5,…,a100=100+101,
∴数列{an}前100项之和为:-(1+2)+(2+3)-(3+4)+(4+5)-…+(100+101)=-1+101=100.
故选B.
|
∴n∈N*,f(n)的值依次为:12,-22,32,-42,52,-62,72,-82,…
∵an=f(n)+f(n+1),
∴a1=12-22=-1-2,a2=-22+32=2+3,a3=32-42=-3-4,a4=-42+52=4+5,…,a100=100+101,
∴数列{an}前100项之和为:-(1+2)+(2+3)-(3+4)+(4+5)-…+(100+101)=-1+101=100.
故选B.
点评:本题考查了错位相减法进行数列求和,还考查了分类讨论的数学思想方法,本题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
曲线
+
=1与曲线
+
=1(k<9)的( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
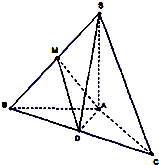 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=
