题目内容
定义在R上奇函数f(x)满足,当x>0时,f(x)=2014x+log2014x,则方程f(x)=0实解个数为( )
| A、1 | B、2 | C、3 | D、5 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:首先,根据奇函数的性质,得到f(0)=0,然后,当x>0时,在同一坐标系内画出函数y=-2014x和y=log2014x,可以得到图象有一个交点,得到方程有一个实根,然后,根据对称性得到相应的方程的根的个数.
解答:
解:∵在R上的奇函数f(x),
∴f(0)=0,
∴x=0是方程f(x)=0的一个实根,
当x>0时,f(x)=2014x+log2014x=0,
∴-2014x=log2014x,
设函数y=-2014x y=log2014x,
在同一坐标系中作出它们的图象如下:
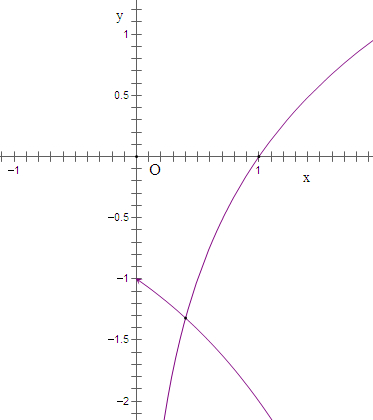
∴当x>0时,该方程有一个实根,
又∵函数为奇函数,
∴它们的图象关于坐标原点对称,
∴当x<0时,该方程也有一个实根,
总之,该方程有三个实根,
故选:C
∴f(0)=0,
∴x=0是方程f(x)=0的一个实根,
当x>0时,f(x)=2014x+log2014x=0,
∴-2014x=log2014x,
设函数y=-2014x y=log2014x,
在同一坐标系中作出它们的图象如下:

∴当x>0时,该方程有一个实根,
又∵函数为奇函数,
∴它们的图象关于坐标原点对称,
∴当x<0时,该方程也有一个实根,
总之,该方程有三个实根,
故选:C
点评:本题综合考查了函数为奇函数及其性质,属于中档题,掌握数形结合思想在求解问题中的灵活运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
二次不等式ax2+bx+c≥0的解集为空集的条件是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
已知△ABC中,“sinA>
”是“A>
”的( )
| 1 |
| 2 |
| π |
| 6 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f(x)(x∈R)满足f(1)=1,f′(x)<
,则不等式f(x2)<
+
的解集为( )
| 1 |
| 2 |
| x2 |
| 2 |
| 1 |
| 2 |
| A、(-∞,-1) |
| B、(1,+∞) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-∞,-1]∪[1,+∞) |
一个树表的生长过程依据图中所示的生长规律,则第15行的实心圆的个数是( )


| A、68 | B、233 |
| C、377 | D、610 |
已知△ABC的三个顶点A,B,C及所在平面内一点P满足
+2
+3
=
,则△BCP的面积与△ABP的面积之比为( )
| BC |
| BA |
| PB |
| 0 |
| A、2:1 | B、3:1 |
| C、3:2 | D、1:2 |
已知P(-1,y)是角θ终边上一点,且sinθ=
,则y的值( )
2
| ||
| 5 |
| A、2 | B、-2 | C、±2 | D、1 |