题目内容
若关于x的方程x2-mx+2=0在(1,4)内有两个解,求m的取值范围.
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用,不等式的解法及应用
分析:设f(x)=x2-mx+2,根据关于x的方程x2-mx+2=0在(1,4)内有两个解,建立不等式,即可求出实数m的取值范围.
解答:
解:设f(x)=x2-mx+2,则
∵关于x的方程x2-mx+2=0在(1,4)内有两个解,
∴
,
解得2
≤m<3,
则m的取值范围为:[2
,3).
∵关于x的方程x2-mx+2=0在(1,4)内有两个解,
∴
|
解得2
| 2 |
则m的取值范围为:[2
| 2 |
点评:本题考查方程根的讨论,考查函数与方程思想,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
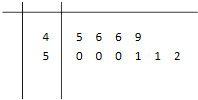 一批食品,每袋的标准重量是50g,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g),并得到其茎叶图(如图).
一批食品,每袋的标准重量是50g,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:g),并得到其茎叶图(如图).