题目内容
5.已知函数y=2${\;}^{-{x^2}+ax-1}}$在[-1,1]上是增函数,则a的取值范围是{a|a≥2}.分析 由题意利用复合函数的单调性,二次函数、指数函数的性质,可得t=-x2+ax-1在[-1,1]上是增函数,可得$\frac{a}{2}$≥1,由此求得a的范围.
解答 解:∵函数y=2${\;}^{-{x^2}+ax-1}}$在[-1,1]上是增函数,
则t=-x2+ax-1在[-1,1]上是增函数,
∴$\frac{a}{2}$≥1,求得a≥2,
故答案为:{a|a≥2}.
点评 本题主要考查复合函数的单调性,二次函数、指数函数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.设角α的终边经过点(-6,-8),则sinα-cosα的值是( )
| A. | -$\frac{7}{5}$ | B. | $\frac{7}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
13.已知二次函数f(x)=ax2+bx+c,若f(0)=f(6)<f(7),则f(x)在( )
| A. | (-∞,0)上是增函数 | B. | (0,+∞)上是增函数 | C. | (-∞,3)上是增函数 | D. | (3,+∞)上是增函数 |
10.程序框图如图所示,其输出的结果为( )

| A. | 2100-1 | B. | 299-1 | C. | 2100 | D. | 299 |
14.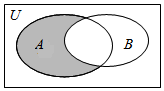 设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
 设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|x≤1} | D. | {x|1≤x<2} |
 如图,有一块半径为2的半圆形空地,计划绿化成等腰梯形ABCD形状的草坪,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设草坪ABCD的周长为y.
如图,有一块半径为2的半圆形空地,计划绿化成等腰梯形ABCD形状的草坪,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设草坪ABCD的周长为y. 如图1,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的“特征三角形”.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.若椭圆C1:$\frac{{x}^{2}}{4}$+y2=1,直线L:y=mx+n
如图1,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的“特征三角形”.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.若椭圆C1:$\frac{{x}^{2}}{4}$+y2=1,直线L:y=mx+n