题目内容
18. 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,若A1C与平面B1BCC1所成的角为$\frac{π}{6}$,则三棱锥A1-ABC的体积为$\frac{\sqrt{2}}{6}$.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,若A1C与平面B1BCC1所成的角为$\frac{π}{6}$,则三棱锥A1-ABC的体积为$\frac{\sqrt{2}}{6}$.
分析 由已知可得A1B1⊥平面BB1C1C,连接B1C,则∠A1CB1为A1C与平面B1BCC1所成的角为$\frac{π}{6}$,求解直角三角形得到BB1,再由棱锥体积公式求得三棱锥A1-ABC的体积.
解答 解:如图,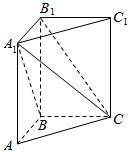
在直三棱柱ABC-A1B1C1中,∵∠ABC=90°,
A1B1⊥平面BB1C1C,连接B1C,则∠A1CB1为A1C与平面B1BCC1所成的角为$\frac{π}{6}$,
∵A1B1=AB=1,∴${B}_{1}C=\sqrt{3}$,
又BC=1,∴$B{B}_{1}=\sqrt{2}$.
∴${V}_{{A}_{1}-ABC}=\frac{1}{3}×\frac{1}{2}×1×1×\sqrt{2}=\frac{\sqrt{2}}{6}$.
故答案为:$\frac{\sqrt{2}}{6}$.
点评 本题考查棱柱、棱锥、棱台体积的求法,考查空间想象能力和思维能力,考查直角三角形的解法,是中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.集合A={x|0≤x<4,且x∈N}的真子集的个数是( )
| A. | 16 | B. | 8 | C. | 15 | D. | 4 |
5.高三(一)班要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同排法的种数是( )
| A. | 1 800 | B. | 3 600 | C. | 4 320 | D. | 5 040 |
2.函数y=f(x)的图象关于直线x=1对称,且在[1,+∞)单调递减,f(0)=0,则f(x+1)>0的解集为( )
| A. | (1,+∞) | B. | (-1,1) | C. | (-∞,-1) | D. | (-∞,-1)∪(1,+∞) |
3.已知函数f(x)满足f(-x)=-f(x),且f(x+2)=f(x),当0≤x≤1时,f(x)=2x(1-x),则f(-$\frac{5}{2}$)=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |