题目内容
设抛物线C:y2=2px(p>0)的焦点为F,经过点F的动直线l交抛物线C于点A(x1,y1),B(x2,y2)且y1y2=-4.
(1)求抛物线C的方程;
(2)若
=2(
+
)(O为坐标原点),且点E在抛物线C上,求△EAB的面积;
(3)若点M是抛物线C的准线上的一点,直线MF,MA,MB的斜率分别为k0,k1,k2.
求证:当k0为定值时,k1+k2也为定值.
(1)求抛物线C的方程;
(2)若
| OE |
| OA |
| OB |
(3)若点M是抛物线C的准线上的一点,直线MF,MA,MB的斜率分别为k0,k1,k2.
求证:当k0为定值时,k1+k2也为定值.
考点:直线与圆锥曲线的综合问题
专题:计算题,压轴题,圆锥曲线的定义、性质与方程
分析:(1)设直线l的方程为x-
=my,与抛物线方程联立消去x,由韦达定理化简可求抛物线的方程;(2)由向量相等表示出点E的坐标,列出方程组,化简求出△EAB的面积;(3)设出点M的坐标,表示出三条直线的斜率,化简可证明.
| p |
| 2 |
解答:
解:(1)点F(
,0),设直线l的方程为x-
=my,
则与y2=2px联立,消去x得,
y2-2pmy-p2=0,
又∵经过点F的动直线l交抛物线C于点A(x1,y1),B(x2,y2)且y1y2=-4.
∴y1y2=-p2=-4,
∴p=2,
∴抛物线C的方程为y2=4x.
(2)∵
=2(
+
)=(2(x1+x2),2(y1+y2)),
∴点E(2(x1+x2),2(y1+y2)),
则由题意得,
,
不妨设m>0,
解得,m=
,|y1-y2|=2
,点E(8,4
),
直线l的方程为2x-
y-2=0,
则|AB|=
×2
=6,
点E到直线l的距离d=
=
,
则S△EAB=
×6×
=3
.
(3)设点M(-1,y),则
k0=
,则y=-2k0,
k1+k2=
+
=
=
又∵y1y2=-4,y1+y2=4m,
则k1+k2=
=
=-y=2k0.
∵k0为定值,
∴k1+k2=2k0也为定值.
| p |
| 2 |
| p |
| 2 |
则与y2=2px联立,消去x得,
y2-2pmy-p2=0,
又∵经过点F的动直线l交抛物线C于点A(x1,y1),B(x2,y2)且y1y2=-4.
∴y1y2=-p2=-4,
∴p=2,
∴抛物线C的方程为y2=4x.
(2)∵
| OE |
| OA |
| OB |
∴点E(2(x1+x2),2(y1+y2)),
则由题意得,
|
不妨设m>0,
解得,m=
| ||
| 2 |
| 6 |
| 2 |
直线l的方程为2x-
| 2 |
则|AB|=
1+
|
| 6 |
点E到直线l的距离d=
|2×8-
| ||||
|
| 6 |
则S△EAB=
| 1 |
| 2 |
| 6 |
| 6 |
(3)设点M(-1,y),则
k0=
| y-0 |
| -1-1 |
k1+k2=
| y1-y |
| x1+1 |
| y2-y |
| x2+1 |
| (y1-y)(my2+2)+(y2-y)(my1+2) |
| (my1+2)(my2+2) |
=
| 2my1y2+2(y1+y2)-m(y1+y2)y-4y |
| m2y1y2+2m(y1+y2)+4 |
又∵y1y2=-4,y1+y2=4m,
则k1+k2=
| 2m(-4)+2×4m-m×4my-4y |
| m2(-4)+2m×4m+4 |
=
| -4(m2+1)y |
| 4(m2+1) |
∵k0为定值,
∴k1+k2=2k0也为定值.
点评:本题考查了圆锥曲线与直线的位置关系,常用到韦达定理及距离公式,化简较复杂,化简要细致,属于难题.

练习册系列答案
相关题目
在边长为2的正三角形ABC中,设
=
,
=
,
=
,则
•
+
•
+
•
等于( )
| AB |
| a |
| BC |
| b |
| CA |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| A、12 | B、-12 | C、6 | D、-6 |
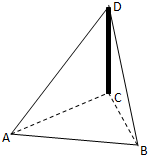 如图所示,哈三中甲,乙两位同学分别站在新校区体育场内的A,B两点,利用三角函数知识测量锅炉房烟囱CD的高.已知AB=15米,∠DAC=60°,∠CAB=15°,∠CBA=45°,求烟囱CD的高.
如图所示,哈三中甲,乙两位同学分别站在新校区体育场内的A,B两点,利用三角函数知识测量锅炉房烟囱CD的高.已知AB=15米,∠DAC=60°,∠CAB=15°,∠CBA=45°,求烟囱CD的高.