题目内容
执行如图所示的程序图,如果输入的t∈[-2,4],则输出的S属于( )


| A、[-7,10] |
| B、[-8,9] |
| C、[-10,7] |
| D、[-9,8] |
考点:程序框图
专题:计算题,算法和程序框图
分析:算法的功能是求S=
的值,根据算法的功能,分段求出S的范围,再求并集.
|
解答:
解:由程序框图知:算法的功能是求S=
的值,
当-2≤t≤2时,S=4t∈[-8,8];
当2<t≤4时,S=6t-t2∈[8,9].
∴输入的t∈[-2,4],则输出的S∈[-8,9].
故选:B.
|
当-2≤t≤2时,S=4t∈[-8,8];
当2<t≤4时,S=6t-t2∈[8,9].
∴输入的t∈[-2,4],则输出的S∈[-8,9].
故选:B.
点评:本题考查了选择结构的程序框图,根据框图的流程判断算法的功能是关键.

练习册系列答案
相关题目
如果复数(m-i)i(其中m∈R)的实部与虚部互为相反数,则m=( )
| A、2 | B、-2 | C、-1 | D、1 |
若复数z满足(1+i)•z=i,则z的虚部为( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知实数x,y满足
,则目标函数z=2x-y的最大值为( )
|
| A、0 | B、3 | C、4 | D、6 |
若(x-
)n展开式的二项式系数之和为64,则展开式的常数项为( )
| 1 |
| x |
| A、10 | B、-20 |
| C、20 | D、-120 |
已知点F(
,0),A(-1,0),B(1,0),直线x=
上有两个动点M,N,始终使∠MFN=45°,三角形MFN的外心轨迹为曲线C,P为曲线C在一象限内的动点,设∠PAB=α,∠PBA=β,∠APB=γ,则( )
| 2 |
| ||
| 2 |
| A、tanα+tanβ+tanγ=0 |
| B、tanα+tanβ-tanγ=0 |
| C、tanα+tanβ+2tanγ=0 |
| D、tanα+tanβ-2tanγ=0 |
已知复数z满足z(1+i)=1(其中i为虚数单位).则z的共轭复数
所对应的点位于( )
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
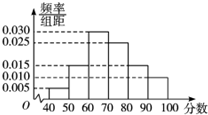 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有600名,据此估计,该模块测试成绩的平均分为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有600名,据此估计,该模块测试成绩的平均分为