题目内容
已知点F(
,0),A(-1,0),B(1,0),直线x=
上有两个动点M,N,始终使∠MFN=45°,三角形MFN的外心轨迹为曲线C,P为曲线C在一象限内的动点,设∠PAB=α,∠PBA=β,∠APB=γ,则( )
| 2 |
| ||
| 2 |
| A、tanα+tanβ+tanγ=0 |
| B、tanα+tanβ-tanγ=0 |
| C、tanα+tanβ+2tanγ=0 |
| D、tanα+tanβ-2tanγ=0 |
考点:轨迹方程
专题:三角函数的求值,圆锥曲线的定义、性质与方程
分析:根据双曲线的第二定义,求出曲线C的方程为x2-y2=1,然后利用两角和的正切公式,即可得到结论.
解答:
解: ∵∠MFN=45°,
∵∠MFN=45°,
∴MN所对的圆心角∠MNP=90°,∠MPC=45°,
即cos∠MPC=
=
=
,
即
=
>1,则根据双曲线的第二定义可知,
三角形外接圆的圆心P的轨迹是以F为焦点,离心率e=
的双曲线,
其中c=
,由e=
=
,解得a=1,b2=c2-a2=1,
即双曲线的方程为x2-y2=1,则y2=x2-1,
∵P为曲线C在一象限内的动点,设∠PAB=α,∠PBA=β,∠APB=γ,
∴设P(x,y),则tan∠PAB=tanα=
,-tan∠PBA=-tanβ=
,
则-tanαtanβ=
•
=
=1,
即tanαtanβ=-1,
tan∠APB=tanγ=tan(180°-α-β)=-tan(α+β)=-
=-
,
即tanα+tanβ+2tanγ=0,
故选:C
 ∵∠MFN=45°,
∵∠MFN=45°,∴MN所对的圆心角∠MNP=90°,∠MPC=45°,
即cos∠MPC=
| PC |
| MP |
| PC |
| PF |
| ||
| 2 |
即
| PF |
| PC |
| 2 |
三角形外接圆的圆心P的轨迹是以F为焦点,离心率e=
| 2 |
其中c=
| 2 |
| c |
| a |
| 2 |
即双曲线的方程为x2-y2=1,则y2=x2-1,
∵P为曲线C在一象限内的动点,设∠PAB=α,∠PBA=β,∠APB=γ,
∴设P(x,y),则tan∠PAB=tanα=
| y |
| x+1 |
| y |
| x-1 |
则-tanαtanβ=
| y |
| x+1 |
| y |
| x-1 |
| y2 |
| x2-1 |
即tanαtanβ=-1,
tan∠APB=tanγ=tan(180°-α-β)=-tan(α+β)=-
| tanα+tanβ |
| 1-tanαtanβ |
| tanα+tanβ |
| 2 |
即tanα+tanβ+2tanγ=0,
故选:C
点评:本题主要考查圆锥曲线的方程的求解以及两角和的正切公式的应用,根据双曲线的第二定义,求出曲线C的方程是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
执行如图所示的程序图,如果输入的t∈[-2,4],则输出的S属于( )


| A、[-7,10] |
| B、[-8,9] |
| C、[-10,7] |
| D、[-9,8] |
已知复数z满足z=
,那么z在复平面上对应的点位于( )
| 2i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数y=sinax+b(a>0)某一个周期的图象如图所示,则函数f(x)=ax2+bx+1零点的个数有( )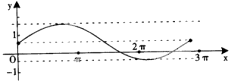

| A、0 | B、1 | C、2 | D、无法确定 |
等差数列{1-3n},公差d=( )
| A、1 | B、3 | C、-3 | D、n |
z=
,则|z|=( )
| 5+12i |
| 3+4i |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知O是坐标原点,点A(-1,0),若M(x,y)为平面区域
上的一个动点,则|
+
|的最小值是( )
|
| OA |
| OM |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
 如图甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图,则甲5次测试成绩的平均数与乙5次测试成绩的中位数之差是
如图甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图,则甲5次测试成绩的平均数与乙5次测试成绩的中位数之差是