题目内容
(x+2)4展开式中含x项的系数等于 .
考点:二项式定理的应用
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于1,求得r的值,即可求得展开式中的含x项的系数.
解答:
解:(x+2)4展开式的通项公式为 Tr+1=
•x4-r•2r,
令4-r=1,求得 r=3,可得开式中含x项的系数为
×2×23=32,
故答案为:32;
| C | r 4 |
令4-r=1,求得 r=3,可得开式中含x项的系数为
| C | 1 4 |
故答案为:32;
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
 某高三学生在高三一轮复习生物学科的22次考试中,所的分数如茎叶图所示,则此同学生物考试分数的极差与中位数之和为
某高三学生在高三一轮复习生物学科的22次考试中,所的分数如茎叶图所示,则此同学生物考试分数的极差与中位数之和为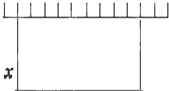 某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=
某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=