题目内容
18.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切.(1)求椭圆E的方程;
(2)H是椭圆E与y轴正半轴的交点,椭圆E上是否存在两点M,N使得△HMN是以H为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
分析 (1)求得原点到直线x-y+$\sqrt{2}$=0的距离d=$\frac{|0-0+\sqrt{2}|}{\sqrt{2}}$=1,从而求得a=2,c=$\sqrt{3}$,b=1;
(2)设能构成等腰直角三角形HMN,其中H为(0,1),从而可设HM所在直线的方程为y=kx+1,(不妨设k>0),则HN所在直线的方程为y=-$\frac{1}{k}$x+1,从而与椭圆的方程联立以解出M,N的坐标,从而求|HM|,|HN|,从而解得.
解答  解:(1)原点到直线x-y+$\sqrt{2}$=0的距离d=$\frac{|0-0+\sqrt{2}|}{\sqrt{2}}$=1,
解:(1)原点到直线x-y+$\sqrt{2}$=0的距离d=$\frac{|0-0+\sqrt{2}|}{\sqrt{2}}$=1,
故b=1,
又∵e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∴a=2,c=$\sqrt{3}$,b=1;
故椭圆E的方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)设能构成等腰直角三角形HMN,其中H为(0,1),
由题意可知,直角边HM,HN不可能垂直或平行于x轴,
故可设HM所在直线的方程为y=kx+1,(不妨设k>0),
则HN所在直线的方程为y=-$\frac{1}{k}$x+1,
由$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$求得交点M(-$\frac{8k}{1+4{k}^{2}}$,-$\frac{8{k}^{2}}{1+4{k}^{2}}$+1),
∴|HM|=$\sqrt{(-\frac{8k}{1+4{k}^{2}})^{2}+(-\frac{8{k}^{2}}{1+4{k}^{2}})^{2}}$=$\frac{8k\sqrt{1+{k}^{2}}}{1+4{k}^{2}}$,
用-$\frac{1}{k}$代替上式中的k得,
|HN|=$\frac{8\sqrt{1+{k}^{2}}}{4+{k}^{2}}$,
由|HM|=|HN|得,k(4+k2)=1+4k2,
∴k3-4k2+4k-1=0⇒(k-1)(k2-3k+1)=0,
解得:k=1或k=$\frac{3±\sqrt{5}}{2}$,
当HM斜率k=1时,HN斜率-1;当HM斜率k=$\frac{3+\sqrt{5}}{2}$时,HN斜率$\frac{-3+\sqrt{5}}{2}$;
当HM斜率k=$\frac{3-\sqrt{5}}{2}$时,HN斜率$\frac{-3-\sqrt{5}}{2}$,
综上述,符合条件的三角形有3个.
点评 本题考查轨迹方程的求解,考查直线与椭圆的位置关系,解题的关键是求出HN、HM的长,利用|HM|=|HN|进行求解.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案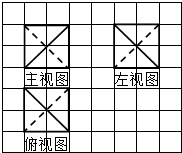
| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
| A. | ($\frac{4}{3}$,$\frac{4}{3}$,$\frac{8}{3}$) | B. | (-$\frac{4}{3}$,-$\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\frac{4}{3}$,-$\frac{8}{3}$) | D. | (-$\frac{4}{3}$,-$\frac{4}{3}$,-$\frac{8}{3}$) |
| A. | x=2 | B. | y=2 | C. | y2=8x | D. | x2=8y |
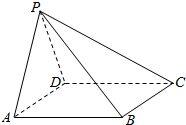 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2.