题目内容
1.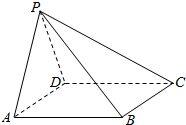 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2.(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
分析 (1)设Q是AD的中点,连接PQ,BQ,通过证明AD⊥平面PBQ,证出AD⊥PB;
(2)利用等体积法,即可求点C到平面PAB的距离.
解答  (1)证明:∵ABCD是菱形,且∠BAD=60°
(1)证明:∵ABCD是菱形,且∠BAD=60°
∴△ABD是等边三角形
设Q是AD的中点,连接PQ,BQ,则BQ⊥AD,
∵△APD是等边三角形
∴PQ⊥AD,
∵PQ∩BQ=Q,
∴AD⊥平面PBQ,
∴AD⊥PB;
(2)解:△PAB中,PA=AB=2,PB=$\sqrt{6}$,S△PAB=$\frac{1}{2}×\sqrt{6}×\sqrt{4-\frac{3}{2}}$=$\frac{\sqrt{15}}{2}$,
设点C到平面PAB的距离为h,则由等体积可得$\frac{1}{3}×\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}=\frac{1}{3}×\frac{\sqrt{15}}{2}h$,
∴h=$\frac{2\sqrt{5}}{5}$.
点评 本题考查空间直线、平面位置关系的判断,考查点面距离的计算,考查空间想象能力、推理论证、计算、转化能力.

练习册系列答案
相关题目
17.已知点A(3,2),B(-2,a),C(8,12)在同一条直线上,则a的值是( )
| A. | 0 | B. | -4 | C. | -8 | D. | 4 |
10.倾斜角是45°且过(-2,0)的直线的方程是( )
| A. | x-y+2=0 | B. | x+y-2=0 | C. | $\sqrt{3}$x-y+2$\sqrt{3}$=0 | D. | $\sqrt{3}$x-y-2$\sqrt{3}$=0 |
11.若直线l1:ax+3y-1=0与l2:2x+y+1=0垂直,则a=( )
| A. | $-\frac{3}{2}$ | B. | $-\frac{2}{3}$ | C. | 6 | D. | -6 |