题目内容
10.定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[-3,-2]时,f(x)=x2+4x+3,则y=f[f(x)]+1在区间[-3,3]上的零点个数为( )| A. | 1个 | B. | 2个 | C. | 4个 | D. | 6个 |
分析 由题意,偶函数f(x)在区间[-3,3]上的值域为[-1,0],确定f(x)=0,即可得出y=f[f(x)]+1在区间[-3,3]上的零点个数.
解答 解:∵当x∈[-3,-2]时,f(x)=x2+4x+3=(x+2)2-1∈[-1,0];
又f(x)为R上的偶函数,
∴当x∈[2,3]时,f(x)∈[-1,0];
又f(x+2)=f(x),∴f(x)为以2为周期的函数,
由题意,偶函数f(x)在区间[-3,3]上的值域为[-1,0],
由f[f(x)]+1=0得到f[f(x)]=-1,于是可得f(x)=0或±2(舍弃),
由f(x)=0可得x=±1,±3,
所以y=f[f(x)]+1在区间[-3,3]上的零点个数为4.
故选:C,
点评 本题考查函数的周期性、奇偶性、函数图象的对称性,体现数形结合的数学思想.考查的知识点是根的存在性及根的个数判断,其中根据已知条件分析函数的性质,进而判断出函数零点的分布情况是解答本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
5.已知集合A={-1,0,1,2},B={x|x<2},则A∩B=( )
| A. | {-1,0,1} | B. | {-1,0,2} | C. | {-1,0} | D. | {0,1} |
2.若函数f(x),g(x)分别是定义在R上的奇函数和偶函数,且满足f(x)+g(x)=ex,则下列结论正确的是( )
| A. | f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$且0<f(1)<g(2) | B. | f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$且0<f(1)<g(2) | ||
| C. | f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$且g(2)<f(1)<0 | D. | f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$且g(2)<f(1)<0 |
19.某企业为了研究员工工作积极性和对待企业改革态度的关系,随机抽取了80名员工进行调查,所得的数据如表所示:
根据上述数据能得出的结论是(参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(b+c)(a+c)(b+d)}$(其中n=a+b+c+d);当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)( )
| 积极支持改革 | 不太支持改革 | 合 计 | |
| 工作积极 | 50 | 10 | 60 |
| 工作一般 | 10 | 10 | 20 |
| 合 计 | 60 | 20 | 80 |
| A. | 有99%的把握说事件A与B有关 | B. | 有95%的把握说事件A与B有关 | ||
| C. | 有90%的把握说事件A与B有关 | D. | 事件A与B无关 |
20.下列函数中,在区间(-1,$\frac{π}{2}$)上单调递减的函数为( )
| A. | y=x2 | B. | y=3x-1 | C. | y=log2(x+1) | D. | y=-sinx |
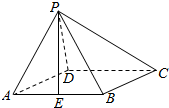 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.