题目内容
已知tan（α+β）=
，tanβ=
，则tan（α+
）的值为 ．
| 2 |
| 5 |
| 1 |
| 3 |
| π |
| 4 |
考点：两角和与差的正切函数
专题：计算题,三角函数的求值
分析：利用tanα=tan[（α+β）-β]，求出tanα，再利用和角的正切公式，求tan（α+
）的值
| π |
| 4 |
解答：
解：∵tan（α+β）=
，tanβ=
，
∴tanα=tan[（α+β）-β]=
=
，
∴tan（α+
）=
=
．
故答案为：
．
| 2 |
| 5 |
| 1 |
| 3 |
∴tanα=tan[（α+β）-β]=
| tan(α+β)-tanβ |
| 1+tan(α+β)tanβ |
| 1 |
| 17 |
∴tan（α+
| π |
| 4 |
| 1+tanα |
| 1-tanα |
| 9 |
| 8 |
故答案为：
| 9 |
| 8 |
点评：本题考查两角和与差的正切函数，考查学生的计算能力，利用tanα=tan[（α+β）-β]，求出tanα是关键．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
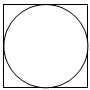一次实验：向如图所示的正方形中随机撒一大把豆子，经查数，落在正方形中的豆子的总数为N粒，其中m（m＜N）粒豆子落在该正方形的内切圆内，以此估计圆周率π为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
下列等式中，成立的是（ ）
A、sin（
| ||||
| B、sin（x+2π）=sinx | ||||
| C、sin（2π+x）=-sinx | ||||
| D、cos（π+x）=cosx |