题目内容
已知:f(x)=cos2x+2
sinxcosx-sin2x,求:
(1)f(x)的最小正周期;
(2)当x∈[0,
]时,求函数f(x)的最大、最小值.
| 3 |
(1)f(x)的最小正周期;
(2)当x∈[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的最值
专题:三角函数的求值
分析:(1)利用三角函数的恒等变换化简函数的解析式为f(x)=2sin(2x+
),再根据函数y=Asin(ωx+φ)的周期
,可得结论.
(2)当x∈[0,
]时,利用正弦函数的定义域和值域,求得函数f(x)的最大、最小值.
| π |
| 6 |
| 2π |
| ω |
(2)当x∈[0,
| π |
| 2 |
解答:
解:(1)∵f(x)=cos2x+2
sinxcosx-sin2x=cos2x+
sin2x=2(
cos2x+
sin2x)=2sin(2x+
),
∴f(x)的最小正周期T=
=π.
(2)∵x∈[0,
]∴2x+
∈[
,
],∴sin(2x+
)∈[-
,1],∴2sin(2x+
)∈[-1,2],
∴f(x)max=2,f(x)min=-1.
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
∴f(x)的最小正周期T=
| 2π |
| 2 |
(2)∵x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
∴f(x)max=2,f(x)min=-1.
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
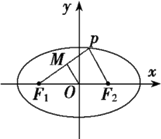 P为椭圆
P为椭圆