题目内容
△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且4sin2
-cos2A=
.
(1)求∠A;
(2)若b=3,c=3,求边a.
| B+C |
| 2 |
| 7 |
| 2 |
(1)求∠A;
(2)若b=3,c=3,求边a.
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)已知等式左边利用二倍角的余弦函数公式化简,再利用诱导公式变形,求出cosA的值,即可确定出A的度数;
(2)利用余弦定理列出关系式,将b,c,cosA的值代入即可求出a的值.
(2)利用余弦定理列出关系式,将b,c,cosA的值代入即可求出a的值.
解答:
解:(1)∵4sin2
-cos2A=2[1-cos(B+C)]-2cos2A+1=
,A+B+C=π,
∴2+2cosA-2cos2A+1=
,
∴cosA=
,
又A∈(0,π),
∴A=
;
(2)∵b=c=3,cosA=
,
∴由余弦定理得:a2=b2+c2-2bccosA=9+9-9=9,
则a=3.
| B+C |
| 2 |
| 7 |
| 2 |
∴2+2cosA-2cos2A+1=
| 7 |
| 2 |
∴cosA=
| 1 |
| 2 |
又A∈(0,π),
∴A=
| π |
| 3 |
(2)∵b=c=3,cosA=
| 1 |
| 2 |
∴由余弦定理得:a2=b2+c2-2bccosA=9+9-9=9,
则a=3.
点评:此题考查了余弦定理,二倍角的余弦函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,
如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,| AP |
| AB |
| AE |
| A、[-1,1] |
| B、[-1,2] |
| C、[-2,1] |
| D、[0,2] |
一般地,在两个分类变量的独立性检验过程中有如下表格:如图是两个分类变量X﹑Y的2×2联表的一部分,则下列说法正确的是( )
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| y1 | y2 | |
| x1 | 15 | 5 |
| x2 | 10 | 15 |
| A、可以在犯错误概率不超过0.025的前提下认为X与Y有关系 |
| B、可以在犯错误概率不超过0.010的前提下认为X与Y有关系 |
| C、可以在犯错误概率不超过0.005的前提下认为X与Y有关系 |
| D、可以在犯错误概率不超过0.001的前提下认为X与Y有关系 |
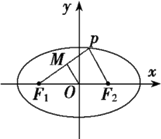 P为椭圆
P为椭圆