题目内容
已知全集为R,集合A={x|2≤x<4},B={x|3x-7≥8-2x},求:
(1)A∩B;
(2)(∁RA)∩(∁RB).
(1)A∩B;
(2)(∁RA)∩(∁RB).
考点:交、并、补集的混合运算,交集及其运算
专题:集合
分析:(1)求出B中不等式的解集确定出B,求出A与B的交集即可;
(2)根据全集R求出A与B的补集,找出两补集的交集即可.
(2)根据全集R求出A与B的补集,找出两补集的交集即可.
解答:
解:(1)∵A={x|2≤x<4},B={x|3x-7≥8-2x}={x|x≥3},
∴A∩B={x|3≤x<4};
(2)∵全集为R,集合A={x|2≤x<4},B={x|x≥3},
∴(∁RA)={x|x<2或x≥4},∁RB={x|x<3},
∴(∁RA)∩(∁RB)={x|x<2}.
∴A∩B={x|3≤x<4};
(2)∵全集为R,集合A={x|2≤x<4},B={x|x≥3},
∴(∁RA)={x|x<2或x≥4},∁RB={x|x<3},
∴(∁RA)∩(∁RB)={x|x<2}.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
一般地,在两个分类变量的独立性检验过程中有如下表格:如图是两个分类变量X﹑Y的2×2联表的一部分,则下列说法正确的是( )
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| y1 | y2 | |
| x1 | 15 | 5 |
| x2 | 10 | 15 |
| A、可以在犯错误概率不超过0.025的前提下认为X与Y有关系 |
| B、可以在犯错误概率不超过0.010的前提下认为X与Y有关系 |
| C、可以在犯错误概率不超过0.005的前提下认为X与Y有关系 |
| D、可以在犯错误概率不超过0.001的前提下认为X与Y有关系 |
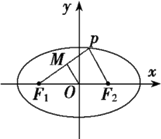 P为椭圆
P为椭圆