题目内容
已知函数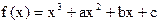 ,曲线
,曲线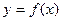 在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为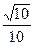 ,若
,若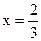 时,
时,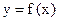 有极值.
有极值.
(I) 求a、b、c的值;
(II) 求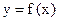 在[-3,1]上的最大值和最小值.
在[-3,1]上的最大值和最小值.
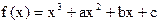 ,曲线
,曲线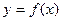 在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为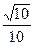 ,若
,若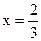 时,
时,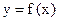 有极值.
有极值.(I) 求a、b、c的值;
(II) 求
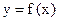 在[-3,1]上的最大值和最小值.
在[-3,1]上的最大值和最小值.(Ⅰ) a=2,b=-4.c=5.
(Ⅱ)f(x)在[-3,1]上的最大值为13,最小值为
(Ⅱ)f(x)在[-3,1]上的最大值为13,最小值为

(I)由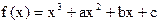 ,得
,得
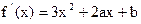 .……………………………………2分
.……………………………………2分
当x=1时,切线l的斜率为3,可得2a+b=0. ①
当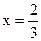 时,
时,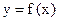 有极值,则
有极值,则 ,可得4a+3b+4=0.②
,可得4a+3b+4=0.②
由①、②解得 a=2,b=-4.……………………………………5分
设切线l的方程为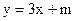 .
.
由原点到切线l的距离为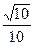 ,
,
则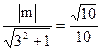 .解得m=±1.
.解得m=±1.
∵切线l不过第四象限,
∴m=1.……………………………………6分
由于l切点的横坐标为x=1,∴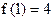 .
.
∴1+a+b+c=4.
∴c=5.…………………………………………………………………7分
(II)由(I)可得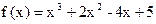 ,
,
∴ .……………………………………8分
.……………………………………8分
令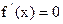 ,得x=-2,
,得x=-2, 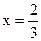 .
.
……………………………………11分
∴f(x)在x=-2处取得极大值f(-2)=13.
在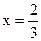 处取得极小值
处取得极小值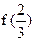 =
= .
.
又f(-3)=8,f(1)=4.
∴f(x)在[-3,1]上的最大值为13,最小值为 .……………………………………13分
.……………………………………13分
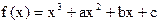 ,得
,得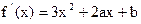 .……………………………………2分
.……………………………………2分当x=1时,切线l的斜率为3,可得2a+b=0. ①
当
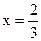 时,
时,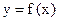 有极值,则
有极值,则 ,可得4a+3b+4=0.②
,可得4a+3b+4=0.②由①、②解得 a=2,b=-4.……………………………………5分
设切线l的方程为
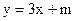 .
.由原点到切线l的距离为
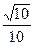 ,
,则
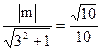 .解得m=±1.
.解得m=±1.∵切线l不过第四象限,
∴m=1.……………………………………6分
由于l切点的横坐标为x=1,∴
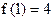 .
.∴1+a+b+c=4.
∴c=5.…………………………………………………………………7分
(II)由(I)可得
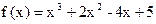 ,
,∴
 .……………………………………8分
.……………………………………8分令
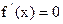 ,得x=-2,
,得x=-2, 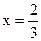 .
.| x | [-3,-2) | -2 | (-2, 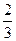 ) ) | 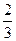 | (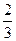 ,1] ,1] |
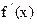 | + | 0 | - | 0 | + |
| f(x) |   | 极大值 |   | 极小值 |   |
∴f(x)在x=-2处取得极大值f(-2)=13.
在
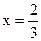 处取得极小值
处取得极小值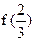 =
= .
.又f(-3)=8,f(1)=4.
∴f(x)在[-3,1]上的最大值为13,最小值为
 .……………………………………13分
.……………………………………13分
练习册系列答案
相关题目
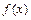 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,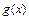 的图象与
的图象与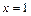 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,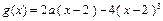 .
.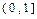 上为增函数,求
上为增函数,求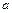 的取值范围;
的取值范围;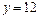 上?若存在,求出
上?若存在,求出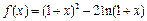 .
.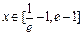 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;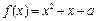 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.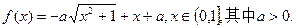
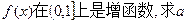 的取值范围;
的取值范围;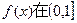 上的最大值.
上的最大值.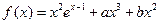 ,已知
,已知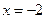 和
和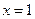 为
为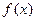 的极值点.
的极值点.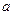 和
和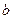 的值;
的值;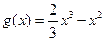 ,比较
,比较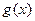 的大小.
的大小. 函数
函数 .
. 的图像关于原点中心对称,则
的图像关于原点中心对称,则 ( )
( ) 上为增函数
上为增函数 上为增函数,在
上为增函数,在 上为减函数
上为减函数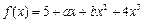 在
在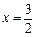 及
及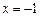 处有极值,
处有极值,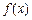 的极值;
的极值;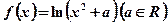 . (1)求在函数
. (1)求在函数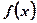 图像上点
图像上点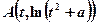 处的切线
处的切线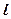 的方程;(2)若切线
的方程;(2)若切线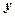 轴上的纵坐标截距记为
轴上的纵坐标截距记为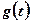 ,讨论
,讨论