题目内容
设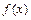 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,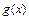 的图象与
的图象与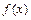 的图象关于直线
的图象关于直线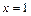 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,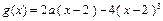 .
.
(1)求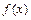 的解析式;
的解析式;
(2)若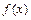 在
在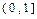 上为增函数,求
上为增函数,求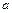 的取值范围;
的取值范围;
(3)是否存在正整数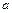 ,使
,使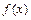 的图象的最高点落在直线
的图象的最高点落在直线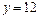 上?若存在,求出
上?若存在,求出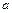 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
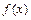 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,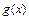 的图象与
的图象与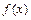 的图象关于直线
的图象关于直线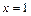 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,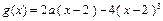 .
.(1)求
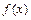 的解析式;
的解析式;(2)若
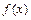 在
在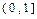 上为增函数,求
上为增函数,求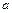 的取值范围;
的取值范围;(3)是否存在正整数
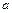 ,使
,使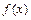 的图象的最高点落在直线
的图象的最高点落在直线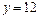 上?若存在,求出
上?若存在,求出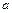 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)∴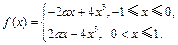
(2)a>(6x2)max=6.
(3)证明见解析。
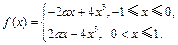
(2)a>(6x2)max=6.
(3)证明见解析。
(1)当x∈[-1,0]时,2-x∈[2,3],f(x)=g(2-x)=-2ax+4x3;当x∈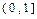 时,f(x)=f(-x)=2ax-4x3,
时,f(x)=f(-x)=2ax-4x3,
∴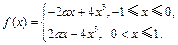 ………………………………………4分
………………………………………4分
(2)由题设知,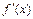 >0对x∈
>0对x∈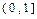 恒成立,即2a-12x2>0对x∈
恒成立,即2a-12x2>0对x∈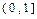 恒成立,于是,a>6x2,从而a>(6x2)max=6.………………………8分
恒成立,于是,a>6x2,从而a>(6x2)max=6.………………………8分
(3)因f(x)为偶函数,故只需研究函数f(x)=2ax-4x3在x∈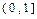 的最大值.
的最大值.
令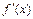 =2a-12x2=0,得
=2a-12x2=0,得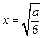 .…10分 若
.…10分 若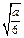 ∈
∈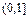 ,即0<a≤6,则
,即0<a≤6,则
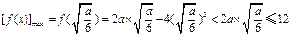 ,
,
故此时不存在符合题意的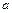 ;
;
若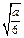 >1,即a>6,则
>1,即a>6,则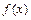 在
在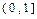 上为增函数,于是
上为增函数,于是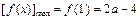 .
.
令2a-4=12,故a=8.综上,存在a = 8满足题设.………………13分
评析:本题通过函数的知识来切入到导数,是在这两个重要知识的交汇处命题,意在考查学生的逻辑思维能力与推理能力,函数及导数的应用是数学的难点,也是考得最热的话题之一,也是本套试卷的把关题,对学生的要求较高.
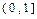 时,f(x)=f(-x)=2ax-4x3,
时,f(x)=f(-x)=2ax-4x3,∴
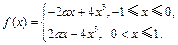 ………………………………………4分
………………………………………4分(2)由题设知,
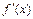 >0对x∈
>0对x∈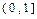 恒成立,即2a-12x2>0对x∈
恒成立,即2a-12x2>0对x∈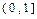 恒成立,于是,a>6x2,从而a>(6x2)max=6.………………………8分
恒成立,于是,a>6x2,从而a>(6x2)max=6.………………………8分(3)因f(x)为偶函数,故只需研究函数f(x)=2ax-4x3在x∈
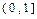 的最大值.
的最大值.令
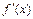 =2a-12x2=0,得
=2a-12x2=0,得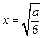 .…10分 若
.…10分 若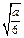 ∈
∈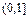 ,即0<a≤6,则
,即0<a≤6,则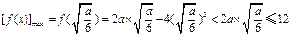 ,
,故此时不存在符合题意的
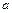 ;
;若
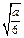 >1,即a>6,则
>1,即a>6,则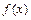 在
在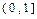 上为增函数,于是
上为增函数,于是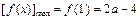 .
.令2a-4=12,故a=8.综上,存在a = 8满足题设.………………13分
评析:本题通过函数的知识来切入到导数,是在这两个重要知识的交汇处命题,意在考查学生的逻辑思维能力与推理能力,函数及导数的应用是数学的难点,也是考得最热的话题之一,也是本套试卷的把关题,对学生的要求较高.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为
 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
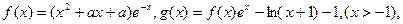
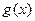 的单调区间,并证明此时方程
的单调区间,并证明此时方程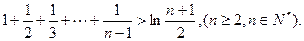
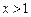 ,求证:
,求证: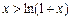 .
.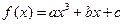
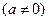 为奇函数,其图象在点
为奇函数,其图象在点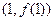 处的切线与直线
处的切线与直线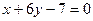 垂直,且在x=-1处取得极值.
垂直,且在x=-1处取得极值.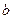 ,
,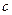 的值;
的值;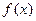 在
在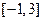 上的最大值和最小值。
上的最大值和最小值。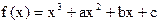 ,曲线
,曲线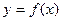 在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为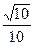 ,若
,若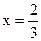 时,
时,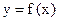 有极值.
有极值.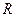 上的奇函数
上的奇函数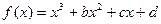 在
在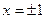 处取得极值.
处取得极值.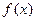 的解析式;
的解析式;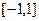 上任意两个自变量的值
上任意两个自变量的值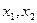 ,都有
,都有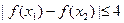 成立;
成立;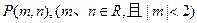 可作曲线
可作曲线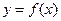 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.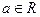 ,
,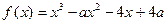 .
.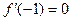 ,求函数
,求函数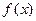 在区间
在区间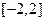 的最大值与最小值;
的最大值与最小值;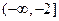 和
和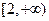 上都是增函数,求实数
上都是增函数,求实数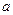 的取值范围.
的取值范围.